序列(Sequence)
單調序列 (Monotonic sequences)
- 令 為實數序列。
- 單調遞增序列(increasing sequence): , .
- 單調遞減序列(decreasing seqeunce): , .
收斂序列 (Convergence sequences)
A sequence in metric space is said to be converge in if there is a point such that:
, .
通常寫為 or .
收斂可解釋為只要夠大,sequence與收斂值之間的差距可以任意小。
If does not converge, it is said to diverge (發散) .
Sequence是否收斂,除了自身的特性外,還必須確認收斂點是否為metric space中的元素。
- E.g. 在會收斂到0,但在, with metric 不收斂,因.
Theorem: Let be a sequence in a metric space ., then
every neighborhood of contains all but finitely many of the terms of .
(收斂的唯一性) Let , and then .
(收斂序列必有界) If converges, then bounded.
If and is a limit point of then there is a sequence in such that .
Sequence 運算
Let and are complex sequences, and then
.
, , .
.
if and .
Subsequence
Subsequence為sequence中不連續的元素(但順序不變)所形成的序列,與演算法中subsequence定義相同。
Definition
- Given a sequence , consider a sequence of positive integers such that then the sequence is called subsequence of .
If every subsequence of converges to .
Theorem: If is a sequence in a compact metric space , then some subsequence of converges to a point of .
Cauchy sequence
Definition
A sequence in m a metric space is said to be a Cauchy sequence if , .
Cauchy sequence可用於判定sequence的收斂性,而不需要知道sequence收斂之值為何。
E.g. are complete metric spaces, 所有的Cauchy sequences均收斂。
- Converge sequence Cauchy sequence。反之不一定成立,必須要加上compact metric space 的條件以保證收斂值位於metric space中。
Properties:
is called bounded set if .
If is a sequence in and consists of the points , then is a Cauchy sequence .
If is the closure of a set , then .
If is a sequence of compact sets in , , and if , then conststs of exactly one point.
發散序列(Divergence sequence)
- 定義: 發散序列( Divergence sequence)
- 令 為實數序列且有以下性質:
- (往正無窮大發散) . usually denoted as .
- (往負無窮大發散) , usually denoted as .
序列的上極限
- 定義: 序列的上極限(upper limit of sequence)
- 令序列 有上界且 則 .
- 若序列 收斂, 則序列 的上極限寫為 .
- 若序列 發散, 則序列的上極限也發散, .
- 若序列 無上界,則序列的上極限發散, .
- .
令為序列的上極限,則必須滿足以下兩個條件:
- .
- 此條件為序列極限有上界,但不唯一。
- .
- .
- 此條件為序列中有無窮多個元素(但非全部)落於的右側。
- 滿足以上兩個條件時,寫為.
- .
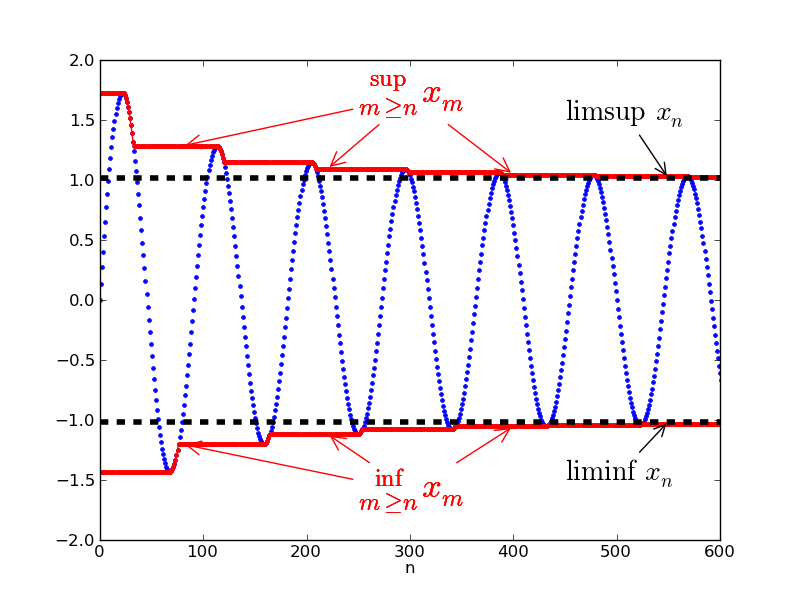
E.g. ,,可知在與間振盪,所以, and .
E.g. is bounded above, and , , .
數列的下極限
- 定義: 序列的下極限(lower limit of sequence)
E.g. .
E.g. .
E.g. .