中間值定理 (Intermediate-value theorem for derivative)
- 令函數,且對於均可微分(有限值或無限大)。令 且 ,若 或 ,則 .
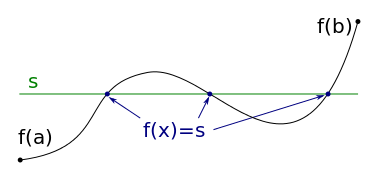
中間值定理。 - Proof:
- Let .
- then .
- 根據連續函數的中間值定理,可知均有定理.
- 根據MVT,可得 for some ,
- 所以在中均有定義。
- TODO
此定理在 或 時仍然成立。
此定義說明了函數的微分值在區間中變號(正值變負值或是負值變正值),則必定存在某一點的微分值為0,且該點為區域極值。
- Corollary: 令函數 在開區間 中每一點均可微(有限值或無限大),且 在端點 與 連續。若 , ,則函數嚴格單調 (嚴格遞增或嚴格遞減)。
- 假設函數為嚴格單調遞增,其微分函數之值必定大於0。
- Corollary: 若函數存在且在開區間單調,則 在開區間連續。
- Proof:(反證法)
- 假設函數在點有跳躍(jump)。
- 令點包含於子區間中。
- 由IVT可知在點應存在微分值,與假設矛盾(QED)。
L'Hospital rule
- 函數在開區間可微分,但在不必可微分,若
- (同時為0、正無窮大或負無窮大)。
- , and .
- then .
此法則可解釋為相對於的增長速度(斜率),經過微分後的比例仍然相等。即位移之值無法比較時,比較速度,若也無法比較時,比較加速度,以此類推。
Taylor's formula
若函數在點可微分,則,即可用線性函數近如下:
- .
若函教 在開區間階可微分,且假設在閉區間連續。假設點,則
- .
Lipschitz condition
- 定義:函數滿足Lipschitz condition of rate 若 (may depend on ) 且 .
若函數滿足此條件,表示函數在開球中均為有限變化量,即不會在點突然變化,所以在點連續(),若,則在點可微分。
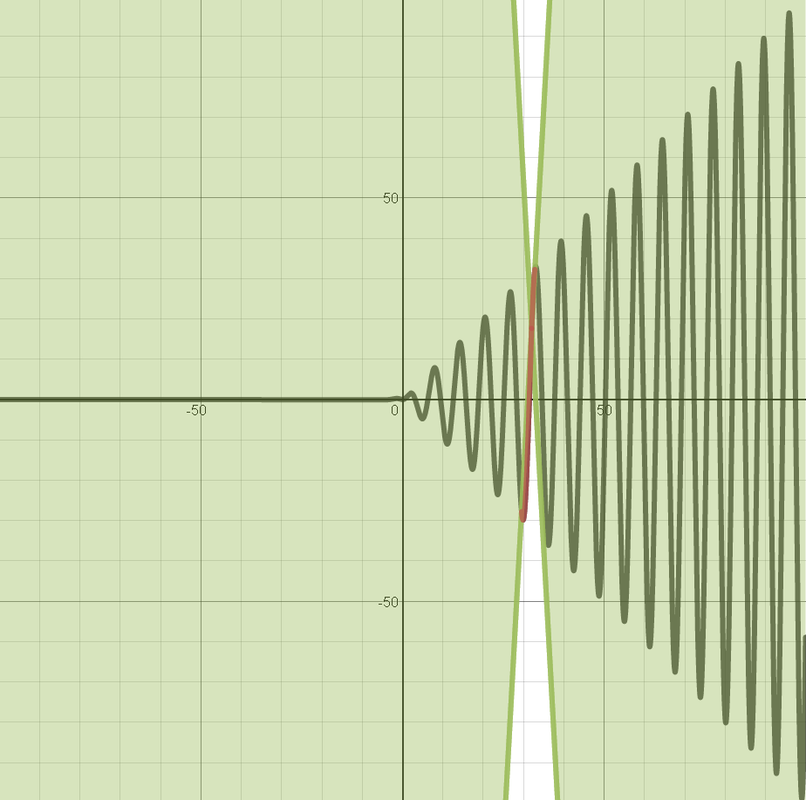
- Uniform Lipchitz condition
- (not depend on ) 且 .
- Uniform與Non-uniform的差別在於是否與的位置有關。
- 時,在區間為常數。
- 時,在區間為有界變分。
Leibnitz's formula
- .
- .