實數中的集合
- 分析數學中的主要概念,如收斂性、微分與積分等,對其討論時,必定都將追溯到實數系的基本性質。
- 我們需證明實數集合R 為一個具有完備素的有序體(complete ordered field)。
自然數(Natural number)
- 自然數集合 N={1,2,⋯,n,⋯}.
- 有些自然數集合的定義會包含元素0。
Peano 公理(axiom)
- 1∈N。
- 若 n1∈N,則 n2∈N, 這裡 n2 為 n1的繼數(successor);即每個自然數都必定有繼數。
- 1 不為任何自然數的繼數。
- 若 n1,m1∈N and n2=m2 then n1=m1;若兩自然數n1, m1的繼數相等時,則n1=m1。
- (數學歸納)(Mathematical induction) Let S⊂N, 1∈S and n1∈S ⇒ n2∈S then S=N.
- 根據Peano公設,我們可以為自然數定義加法運算、乘法運算與次序關系,並證明與自然數系相關的各種性質。
- 再來可證明出整數系Z的性質,再由整數系證明有理數系的加法運算、乘法運算與次序關系,且證明有理數系為有序體。
- 最後再由有理數系證明實數系也滿足此性質。
整數 (Integer)
Z=(−N)∪(0)∪N={,⋯,−2,−1,0,1,2,⋯,}.
- 很明顯可知自然數為整數的子集合,N⊂Z.
有理數 (Rational number)
Q={nm∣gcd(m,n)=1,n≠0,m,n∈Z}.
- 有理數必定是由兩個互質(relative prime)的整數所組成。
- 給定任兩個有理數r,s∈Q且r<s,必存在有理數t∈Q且r<t<s.
(e.g. t=2r+s)
無理數 (Irrational number)
- 無理數即實數中,無法表示為有理數之數,定義為集合Γ,主要有以下三種定義法:
- Cantor以收斂有理數數列定義無理數 (converge sequence of rational numbers)。
- Dedekind以分劃(cut)定義無理數。
- Weierstrass以nested interval定義無理數。
- 實數R中所有元素均可用收斂有理數數列表示,即R=Q∪Γ and Q∩Γ=ϕ.
- 任一無理數均可表示為不循環的小數。
Cantor method
- If a converge sequence of rational numbers {an} satisfies limn→∞an=a, a∈Q, then a is a rational number.
- E.g. {2.1,2.1,⋯,2.1,⋯} is the rational number
2.1.
- E.g. {25,2,611,⋯,2n3n+2,⋯} is the rational number 3/2.
- If a converge sequence of rational numbers {an} satisfies limn→∞an=a, a∉Q then a is an irrational number.
- E.g. {1.4,1.41,1.414,1.4142,⋯} is the irrational
number √2.
實數的組成
- N⊂Z⊂Q⊂R.
- Γ⊂R.
- R=Q∪Γ, Q∩Γ=ϕ.
- R=A∪T, A∩T=ϕ, A為代數數集合,T為超越數集合。
- Q⊂A, T⊂Γ.
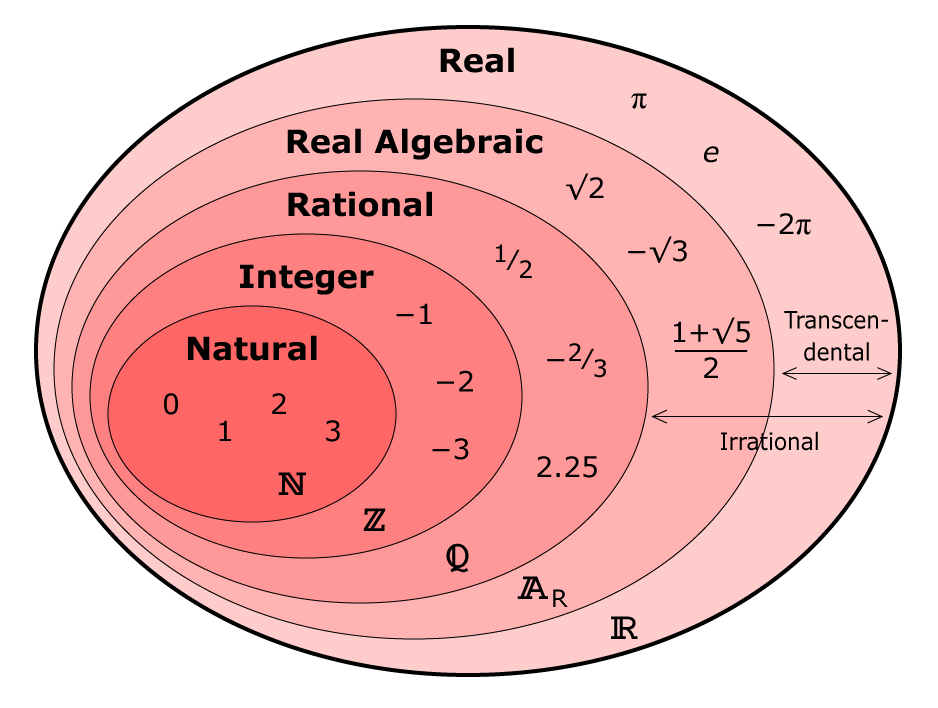 實數集合關係圖.
實數集合關係圖.
