內點與開集

• $\forall x \in \mathbb{R}^k, \ r > 0$
  • 開球(open ball)： $B_r(x) = \lbrace y \in \mathbb{R}^k | \Vert y- x \Vert < r \rbrace$。
  • 閉球(closed ball)： $\overline{B_r}(x) = \lbrace y \in \mathbb{R}^k | \Vert y- x \Vert \leq r \rbrace$
  • 球面(sphere)： $S_r(x) = \lbrace y \in \mathbb{R}^k | \Vert y- x \Vert = r \rbrace$
  • 雖然定義取名為球(ball)，但若度量函數非2-norm時，其形狀不一定為圓形，如1-norm時為菱形，infinity-norm時為方形。
  • 開球是鄰域的特例，因為開球中 $r > 0$，即球中不會只有 $x$ 一點。
• 定義：內點
  • 設 $S \subset \mathbb{R}^k,\ x \in \mathbb{R}^k$.
  • 若存在 $r > 0 \ni B_r(x) \subset S$，則稱點 $x$為集合 $S$的內點(interior point)。
  • 集合 $S$的所有內點所成的集合稱為集合 $S$的內部(interior)，記為 $S^0$。
  • 若存在 $r > 0 \ni B_r(x) \subset \mathbb{R}^k - S$，則稱點 $x$ 為集合 $S$的一個外點(exterior point)，集合 $S$的所有外點所成的集合稱為集合 $S$ 的外部(exterior)，以　$S^e$ 表示。
  • $\forall r > 0, \ B_r(x) \cap S \neq \phi \text{ and } B_r(x) \cap ( \mathbb{R}^k - S) \neq \phi$，則稱點　$x$是集合 $S$的邊界點 (boundary point)。
  • 集合 $S$的所有邊界點所成的集合稱為集合 $S$的邊界(boundary)，以 $S^b$表示。

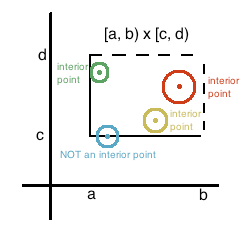
• E.g. $\forall a, b \in \mathbb{R}, \ a < b, [a,b], [a,b), (a,b], (a,b)$等區間的內部都是 $(a,b)$，外部都是 $(-\infty, a) \cup (b, \infty)$，邊界都是 $\lbrace a, b \rbrace$。

• E.g. $S = \lbrace (x,y) \in \mathbb{R}^2 | xy \geq 0 \rbrace$, 則 $S$是兩坐標軸以及第一、三象限內所有點所成的集合。 $S$的內部是第一、三象限內所有點所成的集合。外部是第二、四象限內所有點所成的集合，邊界是兩坐標上所有點所形成的集合。

• 根據上述定義，可知 $\forall S \subset \mathbb{R}^k$，以下性質成立：

  • $S^0 \subset S$。(集合的內部為集合的子集合)
  • $S^e = ( \mathbb{R}^k - S)^0$， $S^e \subset \mathbb{R}^k - S$。
  • $S^0, S^e, S^b$ 三個集合兩兩不相交，且 $S^0 \cup S^e \cup S^b = \mathbb{R}^k$。
  • $S^b = ( \mathbb{R}^k - S)^b$。
  • $S^0$ 為開集合。
  • $S^0 = S \Leftrightarrow S$為開集合。
  • $(S^0)^0 = S^0$.
  • $\forall U \subset \mathbb{R}^k \text{ and } U \subset S \Rightarrow U \subset S^0$，即 $S^0$為包含於 $S$的最大開集合。
  • $S \subset Q \Rightarrow S^0 \subset Q^0$.
  • $(S \cap Q)^0 = S^0 \cap Q^0$.
• 定義：開集合(open set)
  • $S \subset \mathbb{R}^k$，若集合 $S$中的每個點都是 $S$的內點時，則稱此集合為開集合(open set)。
  • $\forall x \in S \exists r > 0 \ni B_r(x) \subset S$.
  • E.g. $(a,b)$為實數集合中的開集合。
  • E.g. $\lbrace (x,y) \in \mathbb{R}^2 | x^2 + y^2 < 1$ 為 $\mathbb{R}^2$中的開集。但$\lbrace (x,y) \in \mathbb{R}^2 | x^2 + y^2 \leq 1 \rbrace$不是，因為此集合包含了邊界點。
• Theorem: $\mathbb{R}^k$中的全體開集合構成 $\mathbb{R}^k$上的一個拓樸結構。
  1. $\phi, \mathbb{R}^k$都是 $\mathbb{R}^k$中的開集合。
  2. $\mathbb{R}^k$中的任一組開集合的聯集仍是 $\mathbb{R}^k$中的開集合。
  3. $\mathbb{R}^k$中有限多個開集合的交集仍然 $\mathbb{R}^K$中的開集合。(無限多個開集合的交集可能會收斂至一點，而非開集合)
  • Proof(1)
  • $\because \phi$不含任何點，所以 $\phi$沒有任何點可以做為其邊界，因此 $\phi$為開集合。
  • $\forall x \in \mathbb{R}^k,\ B_1(x) \subset \mathbb{R}^k$，所以 $\mathbb{R}^k$為開集合。(QED).
  • Proof(2)
  • 令 $U_\alpha | \alpha \in I$ 為 $\mathbb{R}^k$中開集所成形的集合族(family)， $U = \cup_{\alpha \in I} U_\alpha$.
  • 若 $x \in U$ 則 $\exists \alpha \in I \ni x \in U_\alpha$.
  • 因為 $U_\alpha$ 為開集合，所以存在 $r > 0 \ni B_r(x) \subset U_\alpha \Rightarrow B_r(x) \subset U$ (QED).
  • Proof(3)
  • 若 $\cap_{i=1}^n U_i = \phi$，則此交集為開集。
  • 令 $\cap_{i=1}^n U_i \neq phi$, 則 $\forall i=1,2, \cdots, n,\ x \in U_i$.
  • 因為 $U_i$ 為開集合， $\therefore \forall i \exists r_i > 0 \ni B_{r_i} (x) \subset U_i$.
  • 令 $r = \min \lbrace r_1, r_2, \cdots, r_n \rbrace \Rightarrow B_r(x) \subset B_{r_i}(x) \subset U_i$.
  • $\therefore B_r(x) \subset U$

• E.g. $\forall n \in \mathbb{N}, \ U_n = \left( \frac{-1}{n}, \frac{1}{n} \right)$ 均為開集合，但是 $\cap_{n=1}^{\infty} U_n = \{0 \}$不是開集合。

• Theorem: $\mathbb{R}^k$中，每個開球都是開集合。
  • Proof:
  • 令 $B_r(x)$ 為 $\mathbb{R}^k$中的開球.
  • $\forall y in B_r(x), \ \Vert y - x \Vert < r \Rightarrow s = r - \Vert y - x \Vert > 0$.
  • 若 $z \in B_s(y) \Rightarrow \Vert z - y \Vert < s$.
  • $\therefore \Vert z -x \Vert \leq \Vert z - y \Vert + \Vert y - x \Vert < s + \Vert y - x \Vert = r$,
  • $z \in B_r(x) \Rightarrow B_s(y) \subset B_r(x)$，即 $y$ 為 $B_r(x)$的一個內點。
  • 因為 $B_r(x)$中每一個點都是內點，所以 $B_r(x)$為開集合 (QED)。
• Theorem:開集合的充要條件。
  • $\phi \neq U \subset \mathbb{R}^k$為非空開集合 $\Leftrightarrow$ $U$ 可表示為一組 $k$維開球的聯集。
  • 表示為可數集的聯集時，使用可數個即足夠。
  • Proof :( $\Leftarrow$)
  • 若 $U$可表示為一組 $k$維開球的聯集，則依前述定理已證明 $U$為開集合 (QED)。
  • Proof ( $\Rightarrow$)
  • 若 $\phi \neq U \subset \mathbb{R}^k$為非空開集合，則依開集合定義， $\forall x \in U \exists r > 0 \ni B_{r_x}(x) \subset U$，可得出 $U = \cup \lbrace B_{r_x}(x) | x \in U \rbrace$ (QED).
• Theorem:上述定理在實數時可用更直覺方式表示。
  • i 實數 $\mathbb{R}$ 中的每個非空開集合都可以表示為可數個兩兩不相交的開區間之聯集。(開區間可為有限或無限個）
  • Proof:
  • 令 $U \subset \mathbb{R}$為一個非空開集合。
  • $\forall x \in U$，考慮包含於 $U$且包含 $x$ 的所有開區間所形成的集合族 $I_x = \lbrace (a,b) | x \in (a,b) \subset U \rbrace$.
  • $\because x \in U^0 \therefore \exists r > 0 \ni (x-r, x+r) \subset U$, 所以 $I_x$不是空集合。
  • 因為 $I_x$的每個開區間都包含 $x$，所以 $I_x$中所有開區間的聯集仍然是一個包含 $x$的開區間，記為 $(a(x), b(x))$, $\therefore x \in (a(x), b(x)) \subset U$.
  • $\therefore U \ cup \lbrace (a(x), b(x)) | x \in U \rbrace$.
  • 若 $x, y \in U$ 且 $(a(x), b(x)) \cap (a(y), b(y)) \neq \phi$，則其聯集 $(a(x), b(x)) \cup (a(y),b(y))$為一開區間，其包含 $x$且包含於 $U$，因此為 $I_x$的元素。
  • 依定義可知 $(a(x), b(x)) \cup (a(y), b(y)) \subset (a(x), b(x))$ 則 $(a(y), b(y)) \subset (a(x), b(x))$.
  • 同理可得 $(a(x), b(x)) \subset (a(y), b(y))$, 因此對於 $U$中任意兩點 $x,y$，兩區間 $(a(x), b(x)), (a(y), b(y))$只有重合或是不相交兩種可能關係。
  • 在 $U$中選取一子集 $V$ 使得 $\lbrace (a(x), b(x)) | x \in V \rbrace$中每一對開集合區間都兩兩不相等，且 $\lbrace (a(x), b(x)) | x \in V \rbrace = \lbrace (a(x), b(x)) | x \in U \rbrace$，因此 $U = \cup \lbrace (a(x), b(x)) | x \in U \rbrace$ (QED).

• E.g. $(0,1) - \lbrace 2^{-n} | n \in \mathbb{N} \rbrace \subset \mathbb{R}$為一開集合，因為其可表示為 $\cup_{n=1}^{\infty} (2^{-n}, 2^{-n+1}$.

鄰域(Neiighborhood)

• 定義：鄰域(Neighborhood)
  • $\forall x \in \mathbb{R}^k,\ N \subset \mathbb{R}^k$，若 $\mathbb{R}^k$中有開集合 $U$ 滿足 $x \in U \subset N$，則稱 $N$是 $x$的鄰域。
  • 若 $N$是 $x$的鄰域，則 $N - \lbrace x \rbrace$稱為 $x$的一個去心鄰域 (delete neighborhood)。
• Theorem:鄰域與內點的關係
  • $x \in \mathbb{R}^k, \ N \subset \mathbb{R}^k$，則 $N$是 $x$的鄰域 $\Leftrightarrow$ $x$是 $N$的內點。
• Theorem: 鄰域與開集
  • $U \subset \mathbb{R}^k$為非空集合，則 $U$為開集合 $\Leftrightarrow \ U$ 為它所含的每個點的鄰域。
  • 許多性質證明用鄰域會更為方便。
  • Proof ( $\Leftarrow$)
  • 假設 $U$是其所含每個點的鄰域，即 $\forall x \in U$, $U$是 $x$的鄰域，則 $x$是 $U$的內點，所以 $U$中每個點 $x$都是其內點，因此 $U$為開集合。(QED)。
  • Proof ( $\Rightarrow$)
  • 若 U 是開集合，則 $\forall x \in U$，存在開集合 $U \ni x \in U \subset U$，因此 $U$為 $x$
• Theorem:邊界點
  • 點$x \in \mathbb{R}^k$ 是集合 $S \subset \mathbb{R}^k$的邊界點 $\Leftrightarrow$ $x$的每個鄰域都與 $S$相交，也與 $\mathbb{R}^k - S$相交。
• Theorem:鄰域與可數集
  • $A \subset \mathbb{R}^k$，若 $\forall x \in A$，存在鄰域 $N_x \cap A$為可數集時，則 $A$必為可數集。
• 定義：凝聚點(condensation point)
  • $A \subset \mathbb{R}^k,\ x \in \mathbb{R}^k$, 若 $x$的每個鄰域與 $A$的交集都是不可數集，則稱 $x$是 $A$的一個凝聚點。
• Theorem:凝聚點與不可數集
  • $A \subset \mathbb{R}^k$為不可數集，則 $A$必有一個凝聚點屬於 $A$