(積分)均值定理(Mean-value theorem)
- Theorem: 函數為遞增函數,且函數。
- .
- .
- then
- 若函數在區間連續時, for some .
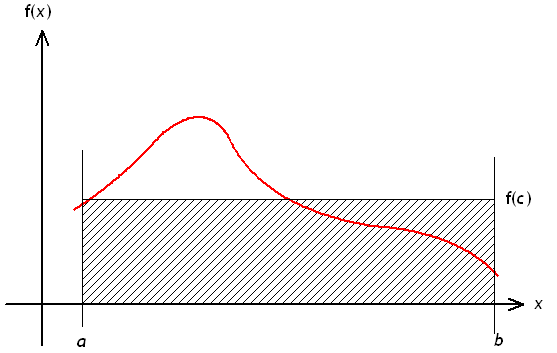
積分均值定理 - Proof:
- 若時,因為積分值為0,所以必定成立。
- 考慮,可得不等式:
- .
- 因此 .
- .
- .(QED)
- Theorem: 函數為連續函數且函數在區間為遞增函數。.
- Proof:
- 由分部積分
- 由均值定理得 (QED).
積分為區間長度的函數
-
Theorem: 函數為有界變分,且函數。令函數.可得
- 在區間為有界變分。
- 在函數上連續的點,在函數上也連續。
- 若函數為遞增函數,當,存在且為連續函數時,微分函數存在,且.
- Proof(1)(2):
- 假設在為遞增函數,所以在此區間為有界變分。
- 若 ,根據MVT可得[1].
- .
- 由[1]可得為有界變分且連續 (QED)。
- Proof (3):
- 將[1]兩側除以 且觀察 as (QED)。
微積分第二基本定理(Second fundmanetal theorem of calculus)
- 令函數;函數,且其微分存在。端點值存在且滿足,則可得.
- Proof:
- 對於的任意分割,可得下式
Given , 分割切的更細後可得以下性質
- (QED)
- 函數,函數且其微分,則下式存在 .
- Proof:
- 由第二基本定理知。
- 由變數變換可得到結果(QED).
Riemann積分變數變換
- 函數,且微分存在。函數且定義。則 ,積分存在且.
Riemann第二積分均值定理
- 函數,且在此區間為遞增函數。令滿足,則
- (Bonnet's theorem) if then
- Proof (1):
- 令,則。
- 根據MVT可得.
- 若且,則(1) 成立。(QED).
- Proof (2), 因為改變函數單點的值不會影響積分的結果,令得證(QED)。
Riemann-Stieltjes積分為函數
在二重積分時,函數給定不同的所對應的到的積分區域均不相同,所以此時積分為的函數;同理給定也會得到不同的積分區域。
- 函數在長方形區間連續。
- 假設函數在區間為有界變分,且函數,則
- 可解釋為, 則 .
- Proof:
- 令為遞增函數。
- 因為為compact set,所以為uniformly continuous on 。
- .
- If ,可得。
- 所以(QED).
- 函數
- 函數
- 定義函數,即
- Proof:
- Let ,則。(QED)
在積分內的微分
- 函數在為有界變分,但是在為定值。
- 假設積分
- 若偏微分在連續,則微分值存在且
- Proof:
- If , then
- .
- 因為在連續,因此得證(QED).
變更積分順序
- 。
- 函數為有界變分,且函數也是有界變分,函數
- 令
- 則 且
- 即