微分 (Derivative)
- 定義:微分
- Function defined on open interval , and , is differentiable at point if
- .
- and radius only depend on .
常用微分符號:
定義在open interval的原因是邊界點不可微分,因微分存在的充要條件是左極限微分值等於右極限微分值。
- 微分的幾何意義是在點切線的斜率,因此不論是從函數左側逼近或是右側逼近,必須要能夠收斂到定值斜率才會唯一存在。
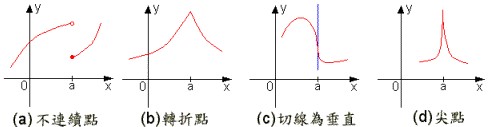
函數中不可微分的點。
微分是對函數的局部變化率的一種線性描述。微分可以近似地描述當函數自變量的取值作足夠小的改變時,函數的值是怎樣改變的。
若函數在某一點無法做到可微,便稱函數在該點不可微。
- 給定的函數在一點的微分如果存在,就一定是唯一的。
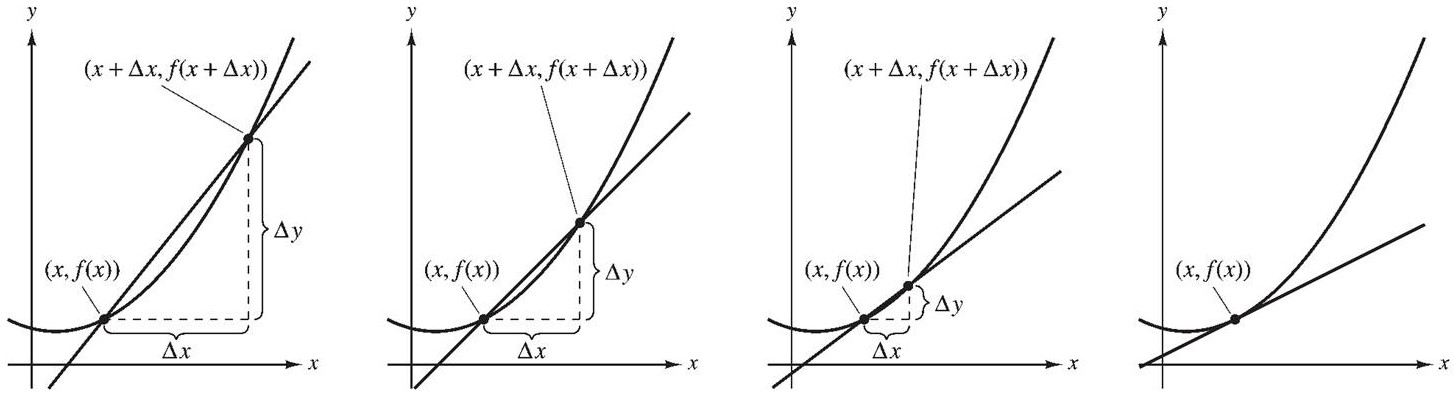
當時,割線逼近於切線。
微分的意義
- Theorem:函數 且在點 可微分, 則存在函數 (depending on and on ) 在點 連續且滿足下式:
- with .
- 反之若在點連續時,且滿足上式,則在點可微分,且.
- Proof :
若存在時,令,當時,。因此在點連續 (QED)。
Proof :
- 且在點連續,則兩側同除且令時,可得存在且等於( QED)。
- Corollary: 函數在點可微分,則在點連續。
E.g. 連續不一定可微,.
- .
- .
- 左極限不等於右極限,因此在此點不可微分。
微分的運算
Functions 與定義在開區間上,則在點可微分,則, , 在點也可微分,若時,也可微分。
- (Additivity) .
- (Chain rule) .
- (Chain rule) .
單邊微分
令函數定義在閉集合 ,則在點左側可微分(lefthand derivative)
- exists.
令函數定義在閉集合 ,則在點右側可微分(righthand derivative)
- exists.
若函數在點可微,則.
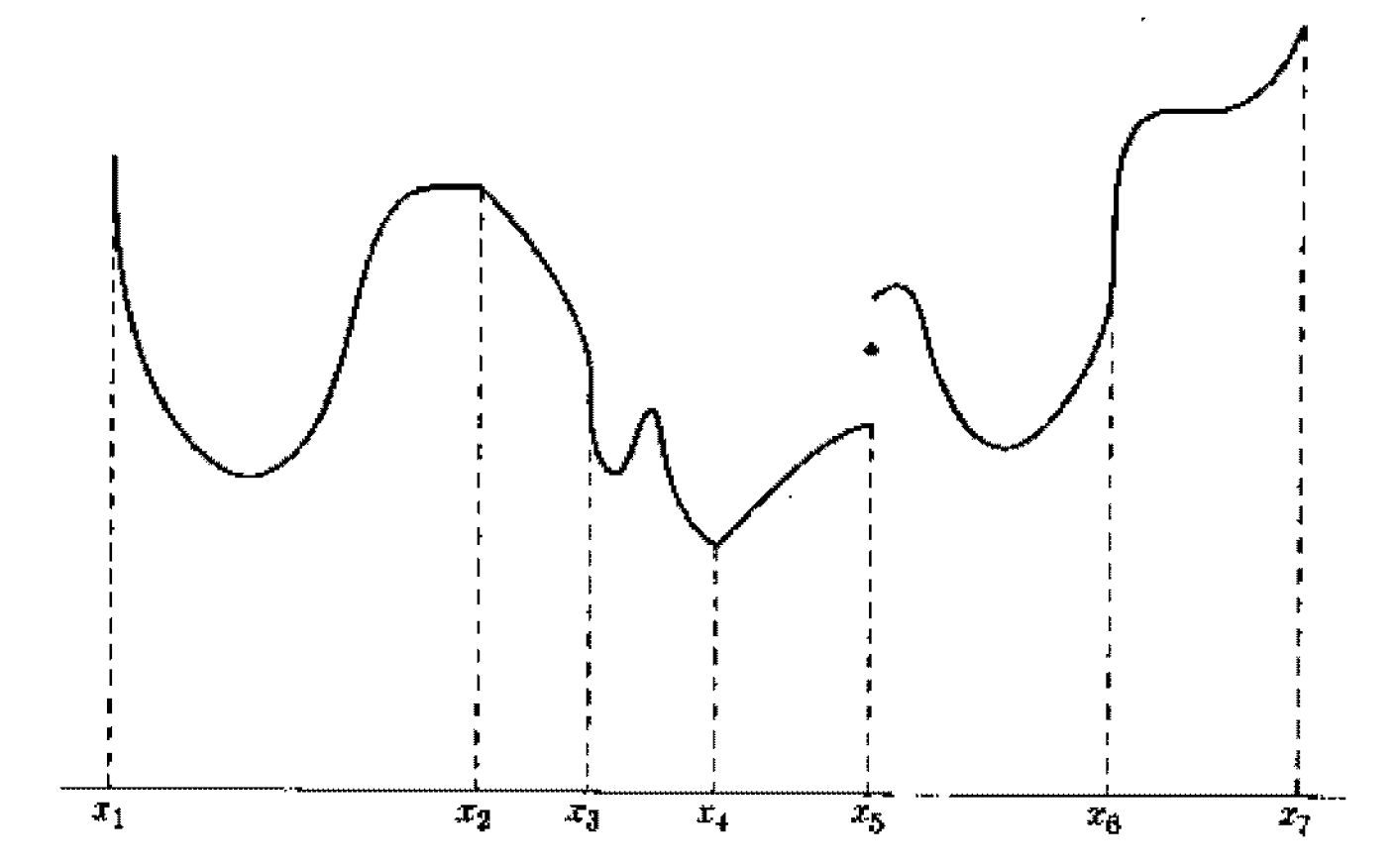
區域極值(local extrema)
令函數 為定義在集合 的實數值函數,,
- 在點 有區域極大值若 .
- 在點 有區域極小值若 .
若函數 定義在開區間 ,且在 中有區域極大值或區域極小值,則 .
Rolle's theorem
- 若函數在開區間 中每一點都可微分,且 在端點與連續,若,則必定存在點.
- Proof(反證法)
- 假設在均不為0。
- 因為函數在compact set 連續,所以必存在最大值與最小值。
- 因為在均不為0 ,所以最大值與最小值必發生在端點中。
- ,即在區間均為常數,但這與假設矛盾 (QED)。
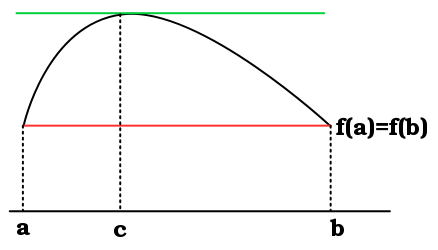
微分均值定理(mean-value theorem for derivatives)
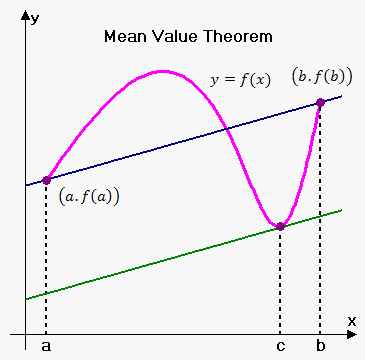
- 令函數 在開區間 中每一點均可微(有限值或無限大),且 在端點 與 連續,則存在點.
幾何的解釋為為一個連接與的平滑函數,而上某一點的微分值必會與線段的斜率相同。
一般化均值定理
- 令函數 在開區間 中每一點均可微(有限值或無窮大)且不存在使得同時為無窮大;且兩函數在端點 與 連續,則存在點.
當時,即為單純的積分均值定理。
Proof:
- Let .
- .
- 當均為有限值時,也為有限值。
- 當其中一個為無窮大時,也為無窮大。
- 由於兩者均為無窮大時為不定型,無法確定的範圍,因此排除此種情形。
- 由定義可知在端點連續,且.
- 根據Rolle's theorem,. (QED)
此定理可再一般化至函數不必在點 或 上連續,只需在這兩點的左、右極限為有限值即可。
- .
- Corollary: 令函數在開區間均可微分(有限值或無限大),且在端點與連續,由MVT可得以下關係。
- 若 ,則 在為嚴格遞增函數。
- 若 ,則 在為嚴格遞減函數。
- 若 ,則 在為常數。 </ul> </div>
- Proof:
- By MVT, (QED)
- 函數,且,則在區間$[a,b]$$為常數。