複數(Complex number)
由於投資組合中,複數的部份只會出現在Fourier transform,因此這邊只簡單介紹複數的運算和意義。
虛數 (Imaginary number)
.
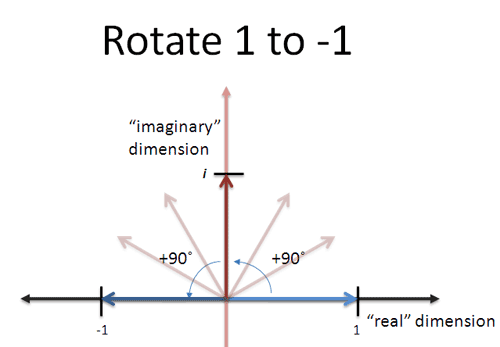
假設有一個數線,上面有兩個反向的點 與 ,可知 旋轉後,就會變成,反之亦然。
旋轉一次,就等於旋轉兩次。
因此可得到以下關係式 (逆時鐘) (逆時鐘 ) ;這邊的代表某種操作,而非乘法。
上式可得 (逆時鐘);令(逆時鐘),可得。
所以可知虛數就是逆時鐘轉, 不是一個數,而是一個旋轉量。
複數的定義(Complex)
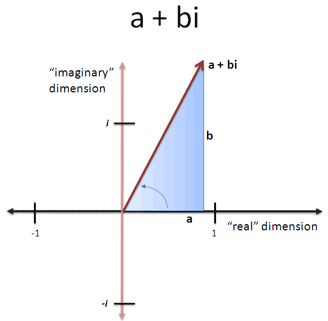
將實數視為軸,虛數視為軸,即構成了二維平面(複數與平面同構(isomorphism),即兩者間存在1-1的函數);旋轉到某一個角度的任何正實數,必定對應平面中的某個點。
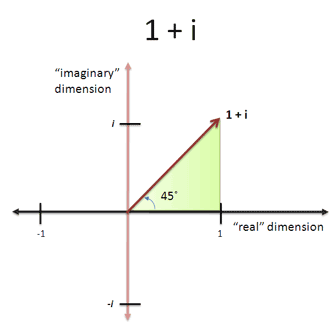
將平面中點,使用表示,此種表示法稱為複數; 為實數部(real number part),為虛數部(imaginary number part)。
- 這邊的加法只是記號,表示實數與虛數的關系,並非算數的加法。
De Moivre定理
- .
Euler 定理
- .