積分函數定義域存在不連續點
當積分函數在區間為常數時,積分 必定存在 (因為在每一個子分割中的)。
而當積分函數在區間為常數,但只在某一點為跳躍值(jump)時,積分積分不一定存在,且存在時也不一定為0。
- Theorem: 給定 ,令積分函數,即 在點 沒有定義。 令函數,若其中至少一個函數於點左側連續且至少一個函數於點右側連續時(左側與右側連續不必為同一函數),則函數在此區間可積分 (或者說當函數在點都不連續時,此時積分不存在),且可得出: (因為在點的左側都是定值,同理在點的右側都是定值,因此只有在跳躍處才有積分值).
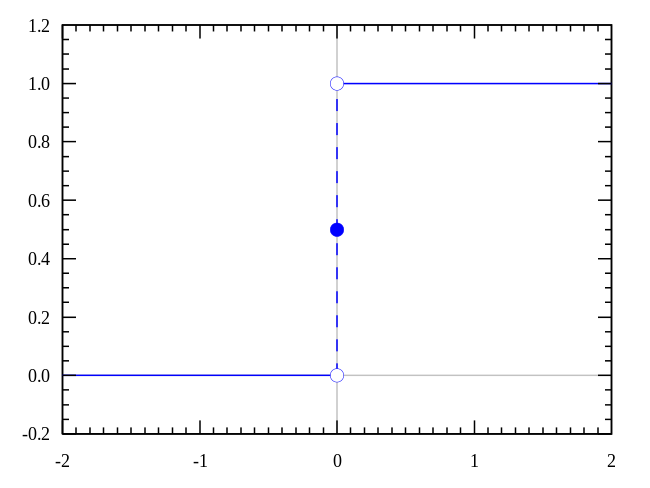
Single point step function . - Proof:
Let ,因此函數除了跳躍點外的值均為0,即, .
為函數在點相對於函數之值,當逼近時,加總應收斂到此值。
令
.
若函數在點連續時, and .
所以可得不等式 ,但此不等式與函數是否在點是否連續無關。
Case 1 (在點連續且函數在點兩側都不連續): 此時 且 時,可得到。
Case 2 (在點右側連續且函數在點左側連續): 必須滿足,即在點右側連續才可得出.
Case 3 (在點左側連續且函數在點右側連續):則必須滿足,即在點左側連續才可得出.
由以上三個case可知除了函數在兩側同時都不連續時才會無法積分(QED).
E.g. , .
- 因為在時,函數,所以.
E.g. 定義同上,但函數,因為在時均無定義,所以不存在。
- , ,上述之值依之值,可能為0, 1, 或-1(無法唯一決定),因此積分不存在。
以有限和表示Riemann-Stieltjes積分
階梯函數(Step function)
- 定義:函數被稱為階梯函數:存在一分割 使得函數在每一個開區間均為常數值。
稱為在點的跳躍(jump),而在端點的跳躍為.
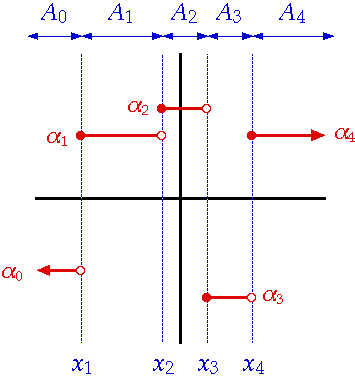
(跳躍點)右連續的階梯函數。
E.g. 最簡單的階梯函數是greatest-integer function,即.
- Theorem: 令為階梯函數,且在之跳躍值為。函數在每一點不會與函數同時在左側或右側不連續,則存在且.
- [1].
- 而且在每一個跳躍點,只要不要同時不連續即可積分 [2]。
- 由[1][2]可得 (QED).
單調遞增的積分函數
- 定義:分割
- ,即第個子分割中,函數的最大值。
- ,即第個子分割中,函數的最小值。
- Upper Stieltjes sum of w.r.t. for partition , .
- Lower Stieltjes sum of w.r.t. for partition , .
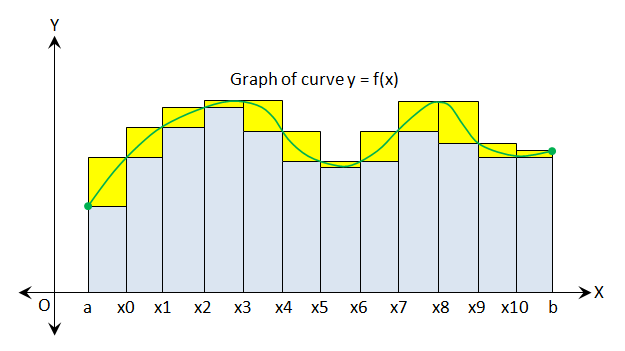
- 由定義可得出 ,若函數在區間為遞增函數,則,因此可得出
- .
- 所以在為遞增函數時,可得.
<<<<<<< HEAD
- Theorem: 若函數為遞增函數,若為更細的分割,則
- (切細時,上總和之值會變小)
- (切細時,下總和之值會變大) =======
- (分割切細時,上總和之值會變小)
- (分割切細時,下總和之值會變大) >>>>>>> 1bd8ee3f8f2acbe338a56a1029e34331a6aec367
- 對於任意兩種分割,可得
Theorem: 若函數為遞增函數,若為更細的分割,則Proof (1)(2):
- 令, then
- ,
- .
- (QED).
Proof (3):
- 令, 可得 . (QED).
Darboux上積分與下積分
- 定義:函數為遞增函數,則
- Upper Stieltjes integral: .
- Lower Stieltjes integral: .
- Theorem: 若積分函數為遞增函數,則下積分之值必定小於等於上積分之值。.
- proof:
- Given .
- 因為為的上界,所以 (QED).
任意函數均可拆成兩個遞增函數的差值,而積分滿足線性相加性質。
E.g. and , then .
- .
上、下積分的線性性質
.
但下式只滿足不等式
- .
- .
Riemann條件
由於上積分之值在定義域切更細的分割時會下降,而下積分之值在定義域切更的分割時會上升,兩者互為上、下界,而在上積分與下積分非常接近時,或是上積分與下積分的差值趨近於零時,可視為等號成立,即積分存在。
- 定義:函數 在閉區間 滿足 Riemann條件 w.r.t. 函數.
此定義即當分割切細時,若函數相對於函數的上、下總和逐漸收斂時,則可積分。
- Theorem: 若函數為遞增函數,則以下三個敘述等價
- 函數。
- 函數在閉區間相對於函數 滿足Riemann條件。
- 函數 Darboux上積分等於下積分,.
Proof from (1) to (2):
- 若時,則(2)一定滿足,因此假設.
- , given . +.
- .
- Given .
- .
- choose
- (QED).
Proof from (2) to (3):
- 若Riemann條件成立,即給定,存在分割.
- .
- [1].
- 在閉區間為遞增函數,所以 [2].
- By[1][2], 可得. (QED).
Proof from (3) to (1):
- 令,要證明 存在且等於。
- 給定,選定分割
- 另外選定分割
- 令 ,可得下式
- (QED).