凸集合(Convex set)
線段 (Line segment)
Line segment between and
- with .
線段有限制長度, 必須在與之間,所以。
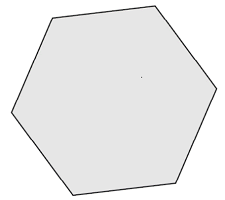
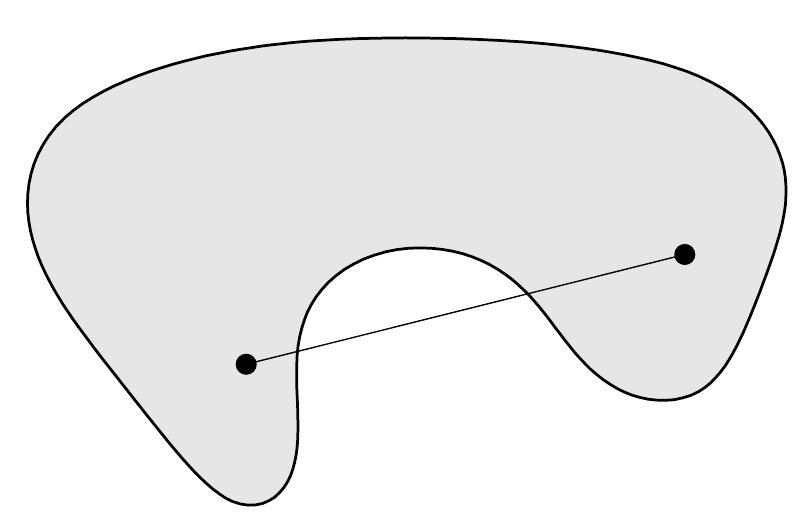
- Convex set contains line segment between any two points in the set.
- , .
仿射集合(Affine set)
Line through .
- .
直線沒有限制長度,所以可為任意實數。
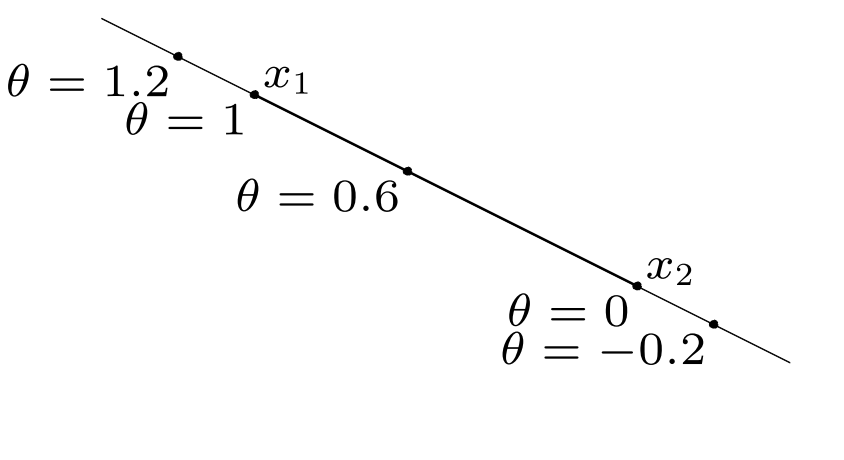
Affine set: contains the line through any two distinct points in the set.
- E.g. solution set of linear equation .
- 反過來說,Affine set可寫做線性方程式的解答集合。
凸組合與凸包(Convex combination and convex hull)
convex combination of
- with
- , .
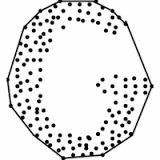
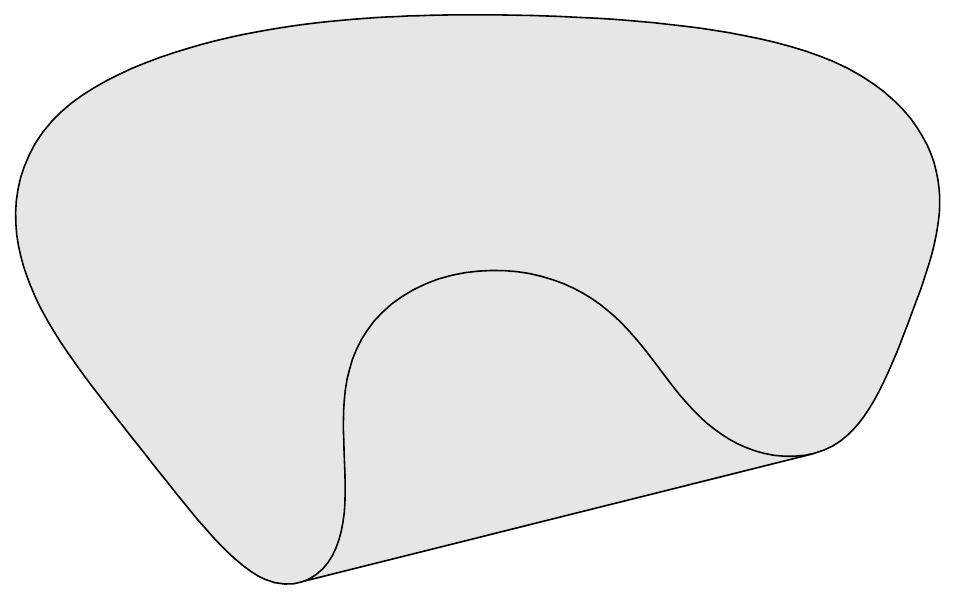
convex hull : set of all convex combinations of points in .
凸錐組合與凸錐(conic combination and convex cone)
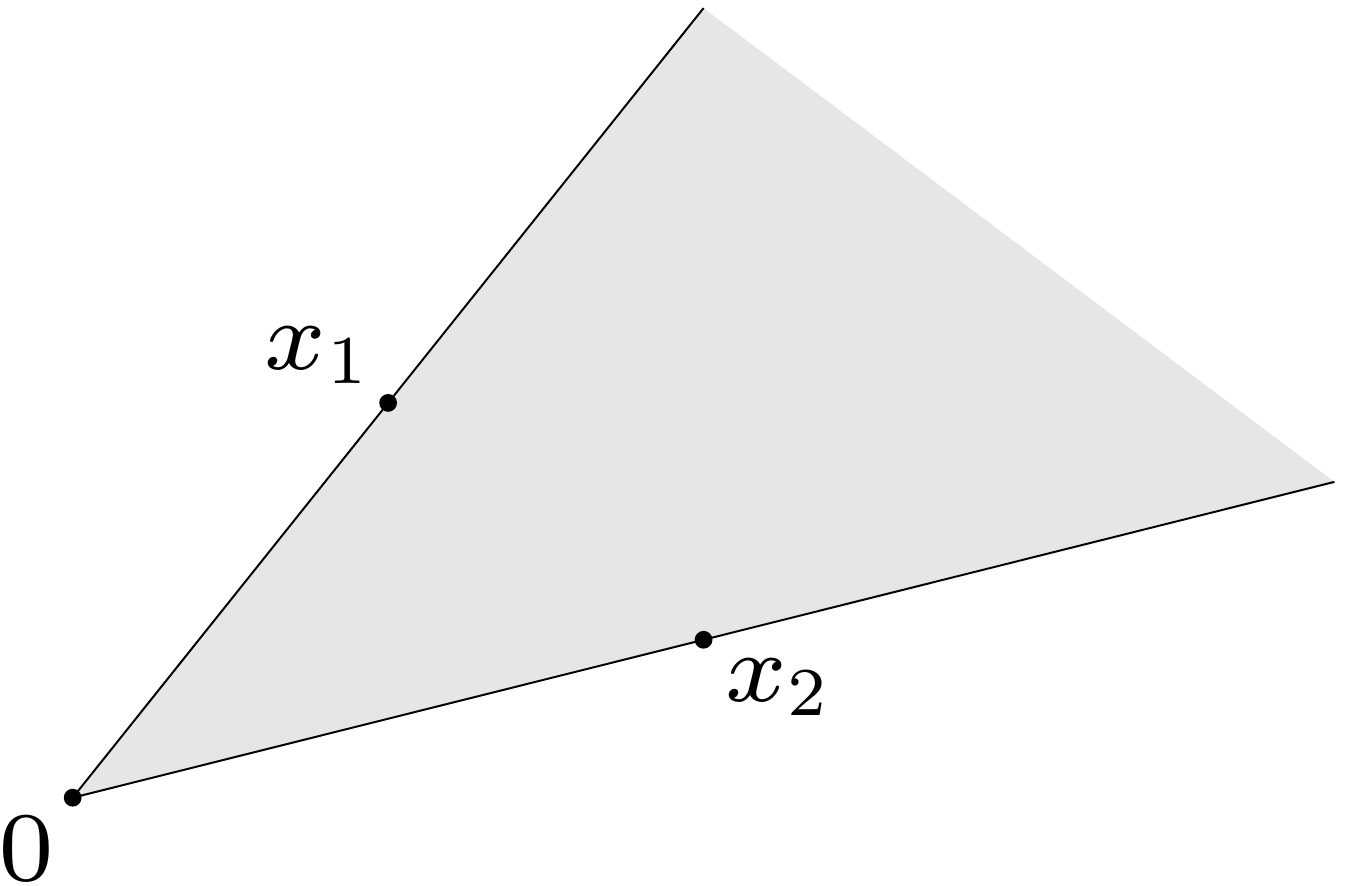
- conic combination of and .
- with and .
- convex cone: set that contains all conic combinations of points in the set.
超平面與半空間(hyperplanes and halfspaces)
- Hyperplane
- .
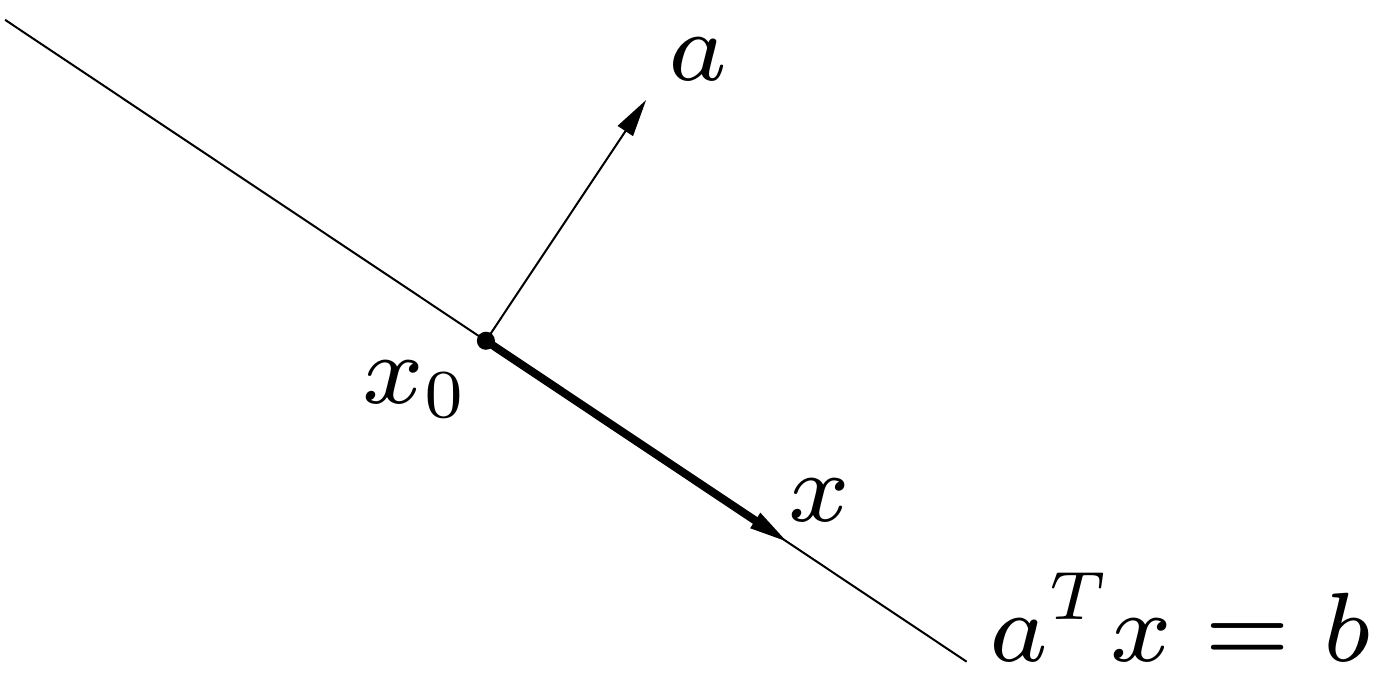
- Halfspace
- .
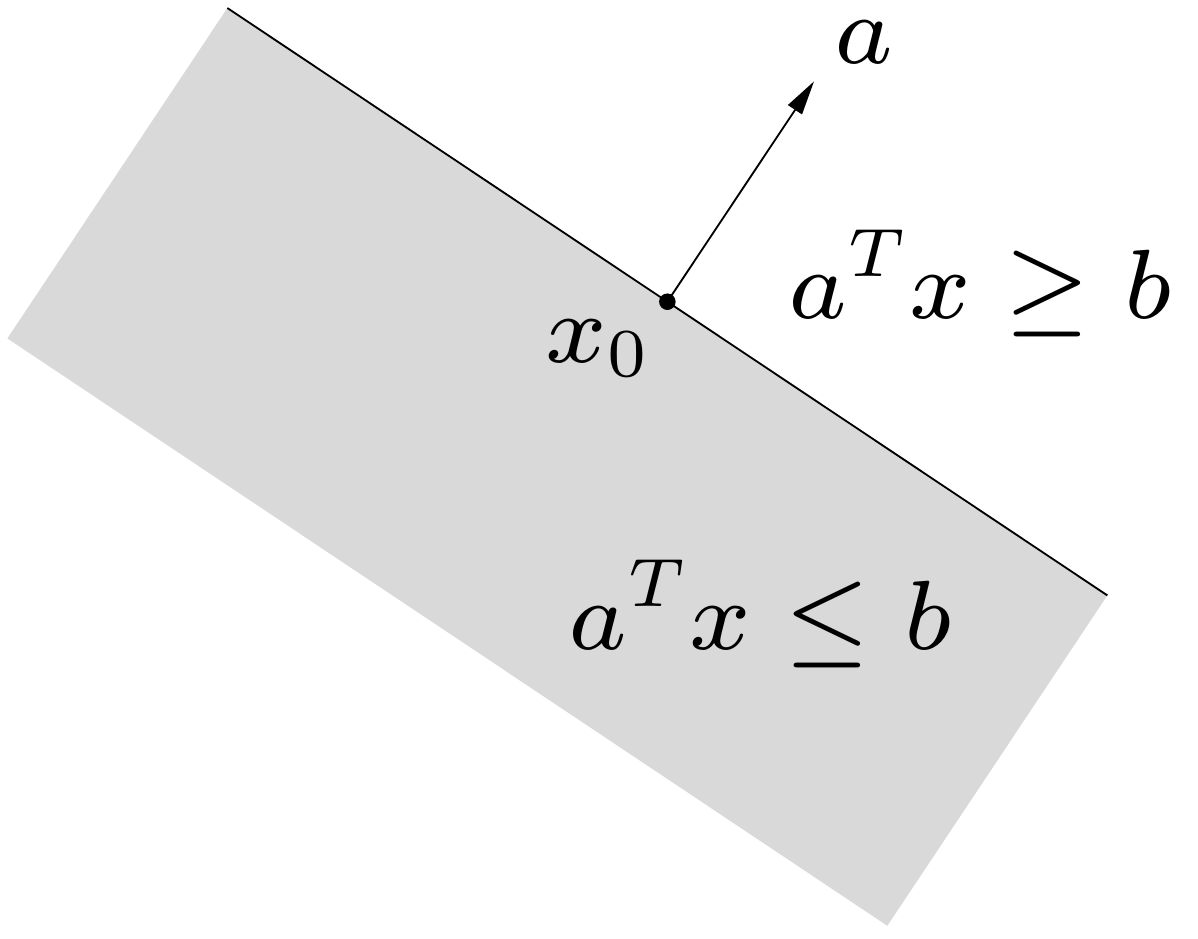
- is the normal vector.
球與橢圓(Ball and ellipsoids)
(Euclidean) ball with center and radius :
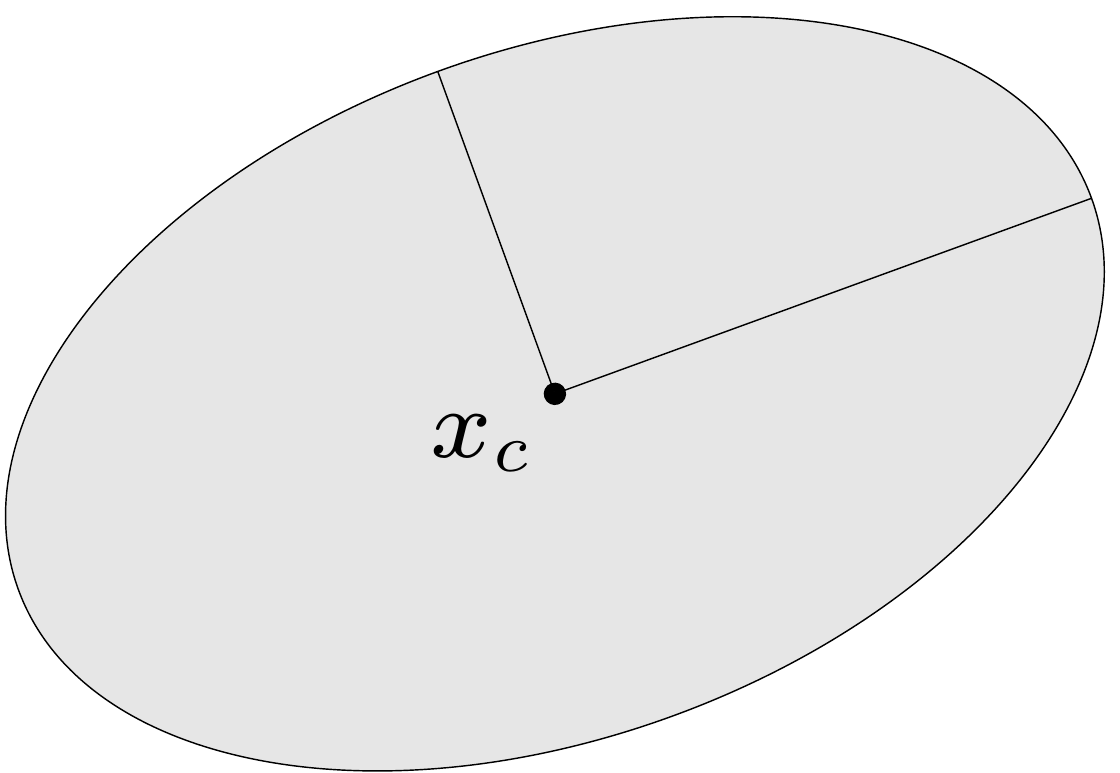
Ellipsoid: set of the form
- .
- ( is symmetric positive definite).
- square and nonsingular.
範數球與錐(norm ball and cone)
for a general norm: .
norm ball with center and radius
- .
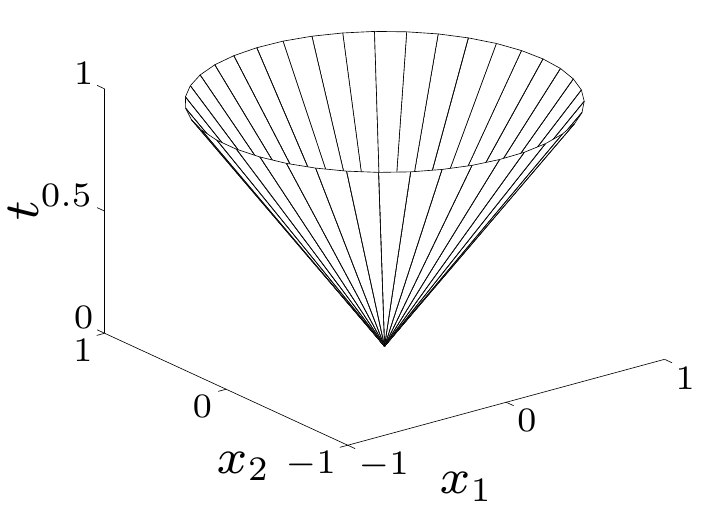
norm cone
- .
Euclidean norm cone常稱為second-order cone.
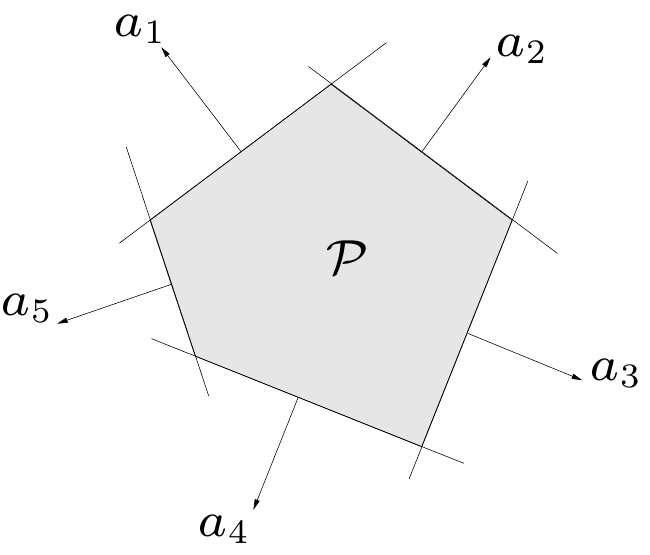
多面體(Polyhedra)
- Solution set of finitely many linear inequalities and equalities.
- , and .
- ,
- 常見於線性規劃的限制式。
正半定錐(Positive semidefinite cone)
- is set of symmetric matrices.
- : positive semidefinite matrices.
- is a convex cone.
- : positive definite matrices.
保留凸性的運算
交集(Intersection)
- 任意數量個的凸集合之交集仍為凸集合。
仿射函數(Affine function)
Suppose is affine function.
E.g. with , .
旋轉 (rotation)、縮放(scaling)、投影(projection)都是仿射運算。
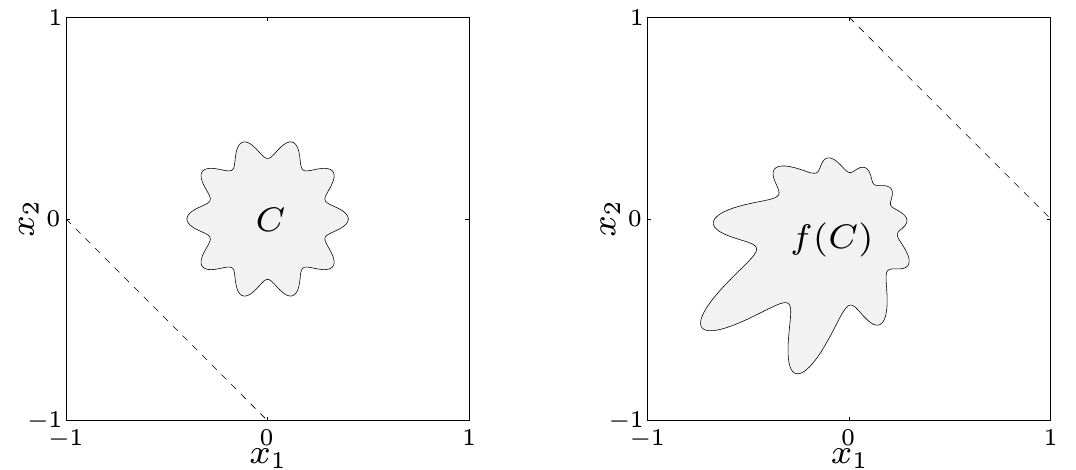
The image of a convex set under is convex.
- is convex is convex.
The pre-image of a convex set under is convex.
- is convex is convex.
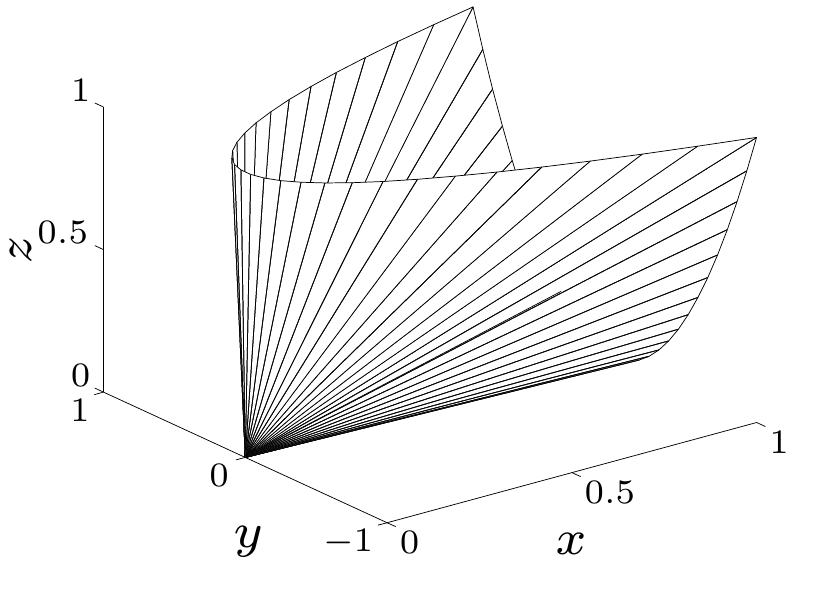
透視函數(Perspective function)
.
- .
- .
Images and pre-images of convex sets under perspective function are still convex.
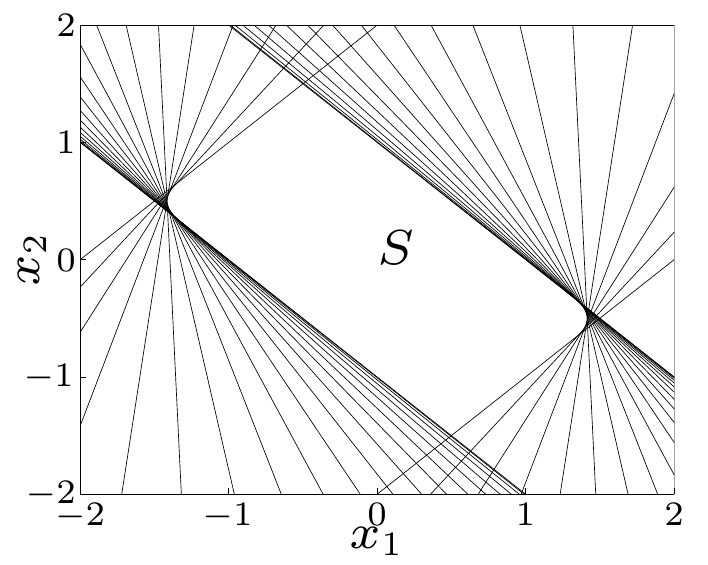
線性分數函數(Linear-fractional function)
- .
- .
- .
Images and pre-images of convex sets under linear-fractional functions are still convex.
E.g. .
- 原始Data envelopment analysis(DEA)的目標函數為線性分數函數,分母為輸入加權值,分子為輸出加權值,而目標函數是要找出給定特徵下,何種輸入、輸出權重可使效率最大化。