深度學習介紹 (Deep learning introduction)

機器學習是仿照人類大腦工作的方式，讓電腦進行計算，學習到類似於大腦的工作方式。為此，研究學者需要構建電腦能夠運作的模型，例如，人工神經網路(ANN)就是根據人類的大腦神經的啟動或抑制的信號傳輸構建的模型。神經網路的基本組成單位就是神經元，神經元的構造方式完全類比了人類大腦細胞的結構。

但是人工神經元只是簡單的結構的模擬，要想達到與生物神經元有相同的功能，還遠遠的不足。許多學者就其訓練的方式對其進行訓練，試圖讓人工神經網路的運算功能盡可能的與人類接近。簡單的網路已經可以進行基本的運算，甚至兩個隱含層的非線性神經網路已經能夠對任意的函數進行平滑的逼近。從 1943年 McCulloch 和 Pitts 提出的簡單神經元開始，神經網路經歷了幾度興衰。但神經網路已經深入到各個領域，且技術相對比較成熟。然而也很難再有新的突破。

為了讓電腦完成人類完成的日常生活中的各種簡單的動作，需要更高度複雜的神經網路來完成。 Hinton等人提出了深度學習，掀起了神經網路研究的又一次浪潮。

深度學習是為了能夠得到有助於理解圖片、聲音、文本等的資料所表述的意義而進行的多層次的表示和抽取的學習。用簡單的機器學習，例如用含2個或 3個隱含層的神經網路，是不可能達到與人類類似的判別決策。因此需要多層的學習器，逐層學習並把學習到的知識傳遞給下一層，以便下層能夠得到更高級別的表述形式，期望可以得到與人類類似的結論。

學習的深度

學習器的深度，決定於學習器的構造。假設學習器為一個有向流通圖，那麼深度就是從起始結點到結束結點（或從輸入結點到輸出結點）的最長路徑。例如，一個支撐向量機(support vector machine, SVM)的深度是2 ，其算法是從輸入端經過一個核變換到核空間，再加上一個線性組合後輸出。再如多層前傳神經網路的深度是隱含層層數加 1(輸出層)。如果說學習到一次知識是一個深度的話，那麼學習的深度是原始資料被逐層學習的次數。

根據學習的深度，機器學習可以分為淺度學習和深度學習。對於簡單的計算，淺度學習可以有效地進行計算，例如二進位資料的邏輯運算。顯然如果想讓機器達到人腦的反應效果，淺度學習是遠遠不夠的，必須要進行深度的機器學習，才有可能得到與人腦反應近似的結果。實際上，深度的機器學習正是模擬了人腦的工作方式。

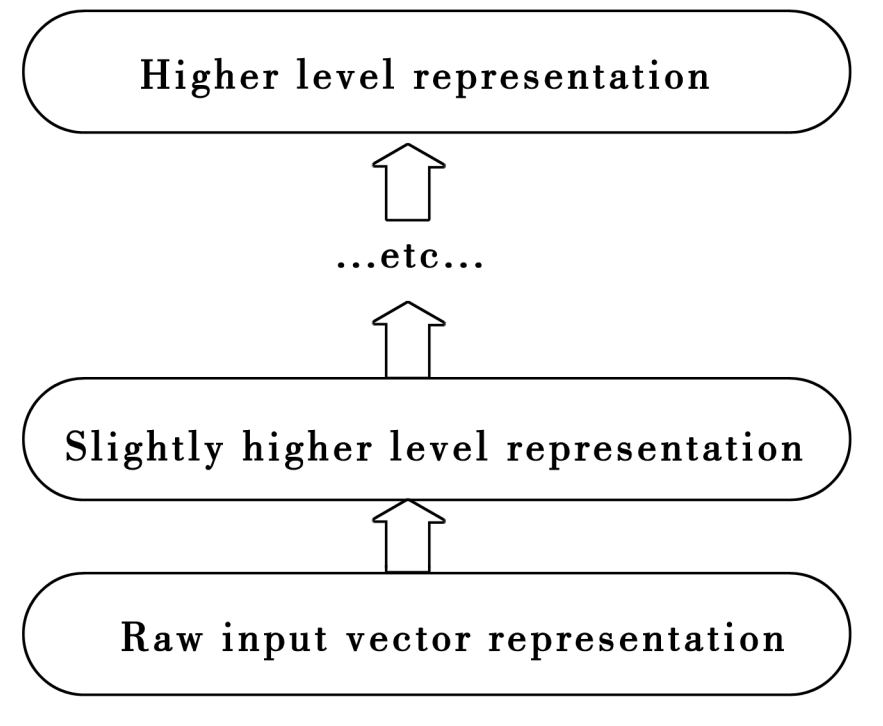
比如要辦識一張含有花朵的圖片，首先由視網膜接受資料信號，視網膜通過神經連結，把看到的圖片轉化成腦波信號傳輸到大腦中，由於大腦的不同部位處理不同的問題，信號不可能一下子就傳到相應位置，需要層層傳輸。同時，在信號傳輸過程中，大腦會提取不同的資訊(特徵)，例如，花的顏色、形狀、個數、位置、個體差異等等。因此，深度的機器學習模型需要具備類似的特徵，即深度的機器學習模型可以提取觀察物件的不同方面的特徵。為此，深度的機器學習模型通常為分層結構，每一層提取資料的1個或多個不同方面的特徵，並把提取出的特徵作為下一層的輸入。

深度學習的動機

從早期的神經網路的學習，到現在的深度學習，究其機制，都是從模擬大腦的構架並輔以一定的學習算法，從而使電腦的工作方式盡可能地接近人類的工作方式。機器學習從僅有2層左右的學習構架，要向有多層的結構發展，不僅有生物神經元的啟示，也是對現有的機器學習結構的弊端的改進。

首先，人類大腦的神經元系統是一個龐大的結構，由無數個神經元共同組成，為了完成一定的生理功能．例如從視網膜到處理視網膜的大腦區域，需要經過無數層的神經元層層傳遞視覺資訊，最終到達大腦的視覺處理區域，然後再經過資訊處理，把資訊回饋到肌肉神經，或語言區域．這個過程在生物神經元系統只不過是瞬間的事情。但是，完成這個過程，是由已經訓練好的神經系統完成的，神經系統對整個過程的處理，與從出生到成人的認知過程是分不開的。而這一切，要用電腦來完成，不是構造簡單的人工神經元就能夠完成的，需要大規模的神經元組織和連結，並經過來自於外界資訊的不斷強化和訓練．故從結構上，神經網路結構要加深。

其次，如果神經網路的層次不夠深，那麼多項式級的參數個數能解決的問題就有可能需要指數級的參數個數。例如要計算 $\Pi_{i=1}^m \sum_{j=1}^n a_{ij}$ ，計算方式不同，計算複雜度會有很大的不同。如果計算和的積，計算複雜度為 $O(mn)$ ；如果計算積的和，計算複雜度為 $O(m^n)$ 。參數多的結構不僅訓練複雜，訓練時間長，而且泛化性能也很差，也容易產生過度擬合(over fitting)問題。

再次，有很多學習結構的學習演算法使得到的學習器是局部估計運算元．例如，由核方法構造的學習器 $f(x) = b + \sum_{i=1}^n a_i \kappa(\mathbb{x}, \mathbb{x}_i)$ ，是由對範本的匹配度加權構成．對於這樣的問題，往往要求被擬合函數都是平滑的，如果不平滑，該學習器就不能很好地擬合資料。而在實際應用中的很多例子，往往不滿足平滑這個條件，或者對於被擬合函數一無所知．此時，範本匹配方法就不再可行。

最後，深度機器學習是資料分散式表示的必然結果。分散式表示系統是由一組資訊計算單元共同完成的，每一個概念都由不止1個資訊計算單元表示，而每一個資訊計算單元也參與計算不止1個概念。例如，表示整數 $i \in \mathbb{N}$ 有2種表達方式；一種用一個 $N$ 維向量 $r(i)$ 表示， $r_j(i)= \begin{cases} 1, & f=i \\ 0, & f \neq i.\end{cases}$ ，，另一種表示方式是用 $\log_2(N)$ 維的向量表示，表示方式類似於二進位。顯然，後一種表示方式更緊湊，這種表示方式就是分散式表示。分散式表示不僅可以很好地描述概念間的相似性，而且合適的分散式表示在有限的資料下能體現出更好的泛化性能。人類的認知活動包括理解和處理接受到的資訊，這些資訊的結構通常很複雜，因此，有必要構造深度結構的學習機器去實現一些人類的認知活動。

由於其自身的複雜性，深度學習演算法很多年都沒有新的進展。就監督的多層神經網路來說，無論是測試精度還是訓練精度，深度學習的結果遠遠不如有１個或２個隱含層的神經網路的結果。直到2006年，Hinton等人提出了貪婪無監督逐層學習演算法，深度學習的問題才有所突破。

Deep learning方法

卷積神經網路（convolutional neural networks, CNN）是一種深度的監督學習下的機器學習模型。
深度置信網（deep belief nets, DBN ）是一種無監督學習下的機器學習模型。

CNN (Convolutional neural networks)

Hubel和Wiesel在60年代研究貓腦皮層時，發現了一種獨特的神經網路結構，可以有效地降低回饋神經網路的複雜性，進而提出了卷積神經網路現在，卷積神經網路已經發展成一種高效的圖像識別方法。

卷積神經網路的基本結構如下所示。卷積神經網路是一種非全連接的神經網路結構，包含２種特殊的結構層：卷積層和次抽樣層。卷積層由多個特徵平面構成，完成抽取特徵的任務。每個特徵平面由神經元構成，在同一個特徵平面上的所有神經元具有相同的連接權重。對於每個神經元，定義了相應的接受域，只接受從其接受域傳輸的信號．同一個特徵平面的神經元的接受域具有相同的大小，故而每個神經元的連接矩陣相同。

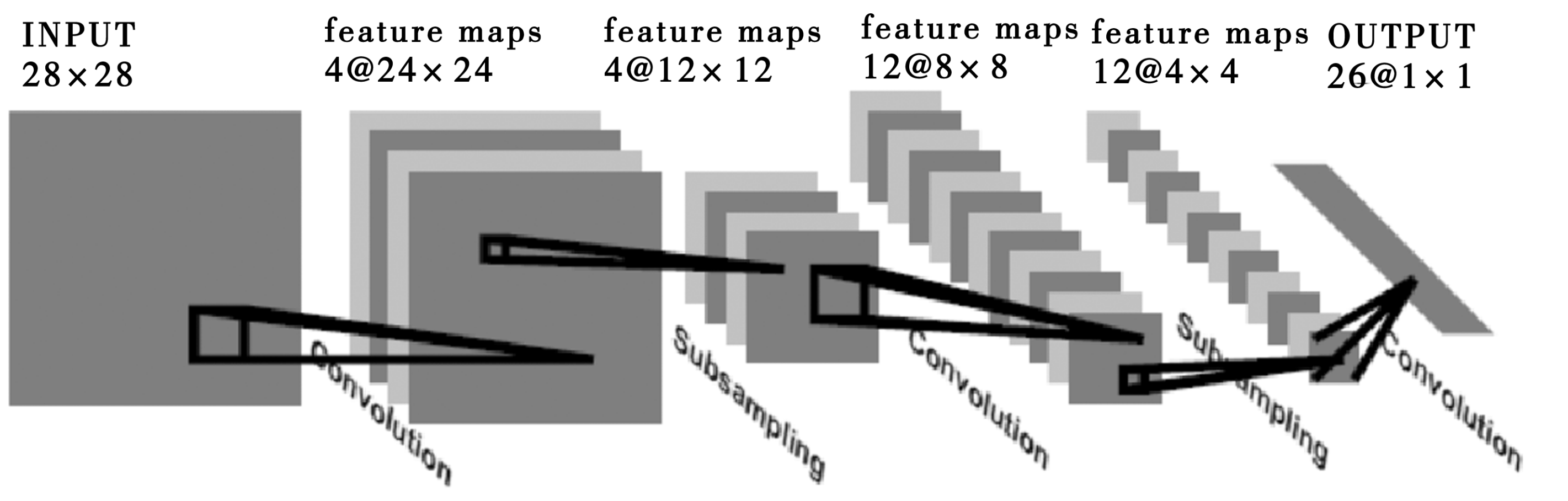
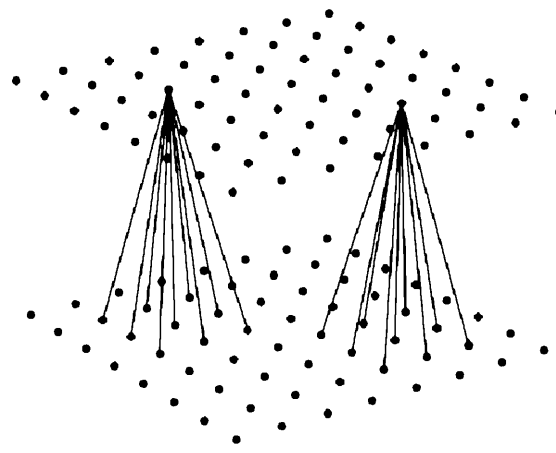
每個卷積層都會緊跟一個次抽樣層。輸入資料經過卷積後，進入高維空間，換句話說，卷積層進行了升維映射。如果不斷地進行升維，則不可避免地陷入維數災難( curse of dimensionality)。同卷積層類似，次抽樣層的每個特徵平面上的神經元也共用連接權重，且每個神經元都從其接受域中接受資料。卷積層的每個特徵平面都對應了次抽樣層的一個特徵平面，次抽樣層中的神經元對其接受域中的資料進行抽樣（例如，取大，取小，取平均值，等等），因此次抽樣層的特徵平面上的神經元的個數往往會減半。

卷積層的每一個平面都抽取了前一層某一個方面的特徵。每個卷積層上的每個結點，作為特徵探測器，共同抽取輸入圖像的某個特徵，例如４５度角、反色、拉伸、翻轉、平移等。圖像經過一層卷積，就由原始空間被影射到特徵空間，在特徵空間中進行圖像的重構。卷積層的輸出，為圖像在特徵空間中重構的座標，作為下一層也就是次抽樣層的輸入。

LeCun從1998年開始，專注於卷積神經網路的研究，提出了LeNet模型，用於識別手寫和打字體，逐漸已經適用識別很多類圖形問題。LeNet模型在識別手寫數位上達到很高的識別率，而且具有拉伸、擠壓、反轉的不變性，而且抗噪能力很強。模型用傳統的BP進行訓練。

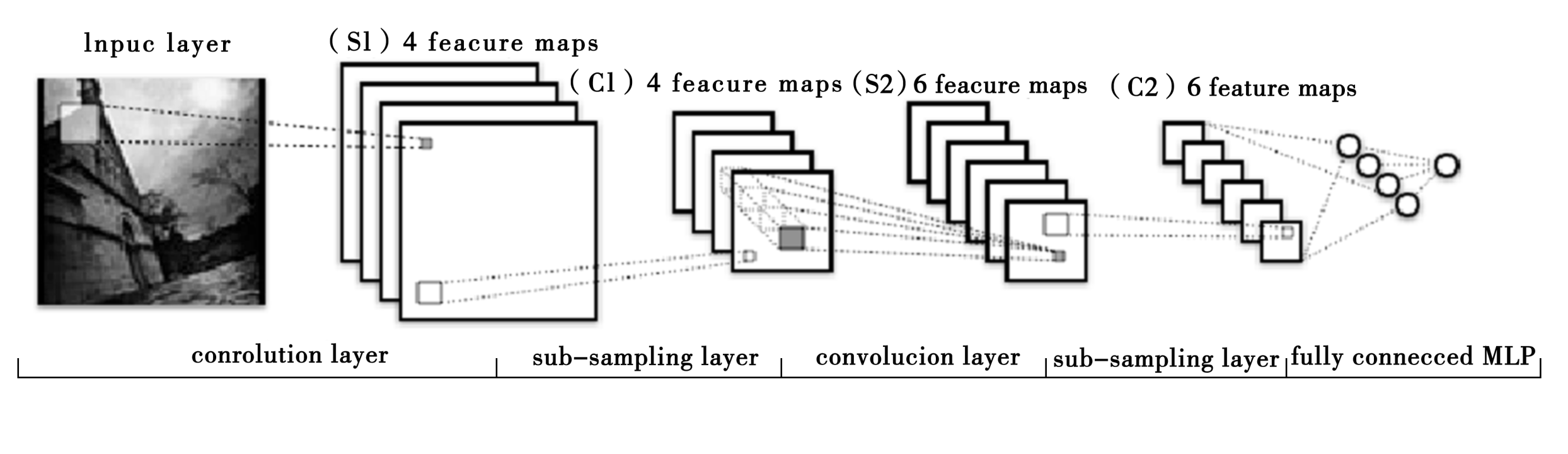
DBN (Deep belief nets)

DBN是另一種由Hintion等學者所提出的深度學習結構，其為是多個 RBM (restricted Boltzmann machine)的累加。一個Boltzmann 機是基於能量理論的概率模型，通過熱力學的能量函式定義了一個機率分佈：Boltzmann 分佈。

假設狀態隨機變數為 $x$ ，能量函數為 $E(x)$ ，則該狀態出現的機率密度函數為 $p(x) = e^{-E(x)}/Z,\ Z=\sum_x e^{-E(x)}$ 。一個典型的Boltzmann機為無向循環圖，其能量函數為 $E(x,h) = -b^{\intop}x - c^{\intop}h -x^{\intop}Wh -x^{\intop}Ux - h^{\intop}Vh$ ，其中 $x$ 是可見變量(通常指輸入的資料)； $h$ 是隱含變量，無法觀察到實際值； $b, h$ 分別為可見戶量與隱含變量的閥值； $W,U,V$ 是結點之間的連接權重。

如果對Boltzmann機給予約束條件，令其自身不與自身連接，則可得一有向無環圖RBM，其能量函數為 $E(x,h) = -b^{\intop} x - c^{\intop}h - x^{\intop}Wh$ 。

一個典型的DBN可以看成是由多個隨機變數組成的有向無環圖，也可以看成是多個RBM的累加，因此DBN就是一個複雜度很高的有向無環圖。Hinton等認為一個具有 $l$ 個隱含層的DBN，可以用聯合機率分佈描述輸入向量 $x$ 與隱含向量 $h$ 間的關係：

$P(x, h^1, h^2,\cdots, h^l) = \left( \Pi_{k=2}^l-2 P(h^k|h^{k+2} \right) P(h^{l-2}, h^t)$ . 其中 $x=h^0$ ； $P(h^k|h^{k+2}$ 是條件機率分佈。

DBN的學習過程，就是學習聯合機率分佈的過程，而聯合機率分佈的學習是機器學習中的generating learning。

對於深度的機器學習，由於參數變數很多，所以合適的訓練演算法直接決定了學習器的性能。以往的基於最速梯度下降的BP (back-propagation)演算法，在經典的神經網路中被廣泛應用，可以得到泛化性能很好的網路結構，但是BP算法對於深度學習器的訓練卻存在一定的困難。這主要是BP演算法本身的約束所在。

首先，BP演算法是監督學習，訓練資料必須是有類標資料。但是，實際能得到的資料大都是無類標資料。
其次，BP演算法不適合有很多隱含層的學習結構，一是計算偏導數很困難，二是誤差需要層層逆傳，收斂速度很慢。
最後，BP演算法經常會陷入到局部最優解，不能到達全域最優解。因此，Hinton等人提出了貪婪的逐層無監督訓練演算法。

貪婪無監督學習演算法的基本思想是，把一個DBN網路分層，對每一層進行無監督學習，最後對整個網絡用監督學習進行微調。把一個DBN網路分層，每層都由若干計算單元（常常是幾百個或幾千個）組成，各自獨立計算該層接受到的資料，每個層的節點之間沒有連接。與外界環境連接的節點層為輸入層，輸入層接受來自於外界的輸入，例如圖像資料。第１層（即輸入層）與第２層構成一個典型的RBM，根據無監督學習調節網路參數，使得RBM達到能量平衡。然後，第１層的輸出作為第２層與第３層構成一個新的RBM，第１層的輸出作為外界輸入，繼續調節參數，使當前RBM結構達到能量平衡。如此進行下去，直到最後一層。當完成無監督逐層訓練學習後，再以原始外界輸入和目標輸出對整個網路進行有監督學習，以最大似然函數為目標，精調網路各層的參數。

Gibbs抽樣技術是在訓練每個RBM時採用的有效隨機抽樣技術。假設要從未知的聯合機率分佈 $f(x_1, x_2, \cdots, x_k)$ 中抽取 $n$ 個樣本 $X^{(1)}, X^{(2)},\cdots, X^{(n)}$ ，由於

$P(x_j | x_1, x_2, \cdots, x_{j-1}, x_{j+1}, \cdots, x_k) = \frac{P(x_1, x_2, \cdots, x_k)}{P(x_1, x_2, x_{j-1}, x_{j+1}, \cdots, x_k)} \propto p(x_1, x_2, \cdots, x_k)$ ,

從而對某一個變數抽取樣本時，假設其他變數已知，在以其他變數為條件的概率分佈下進行抽取，直到抽取出所有樣本。換句話說，對於樣本 $X^{(i)}$ 的第 $j$ 個變量，是從其分佈 $P(x_j^{(i)} | x_1^{(i)}, x_2^{(i)}, \cdots, x_{j-1}^{(i)}, x_{j+1}^{(i)}, \cdots, x_k^{(i)})$ 中抽取，直到抽取出 $n$ 個樣本。

在貪婪學習演算法中，也採用了 Wake-sleep演算法的基本思想。演算法在覺醒階段，採用學習到的權重，按照自底朝上的順序，為下一層產生訓練需要用的資料，而在睡眠階段，按照自頂朝下，用權重對資料進行重建。

以 $x=h^0$ 為外界輸入，訓練第一個RBM達到能量平恆。
用第一層學習到的輸入聯合機率分佈，作為第二層RBM的輸入，繼續相同的訓練。
重覆第二步，直到最後一層。
以MLE為目標函數，調整各層參數，使網路達到最佳化。

參考文獻

1	李海峰 and 李纯果, 深度学习结构和算法比较分析, 2012.
2	Hinton, Geoffrey E and Osindero, Simon and Teh, Yee-Whye, A fast learning algorithm for deep belief nets, MIT Press, 2006.
3	Hubel, David H and Wiesel, Torsten N, Receptive fields, binocular interaction and functional architecture in the cat's visual cortex, Wiley Online Library, 1962.

深度學習介紹(Deep learning introduction)