PAC (Probability Approximately Correct) learning

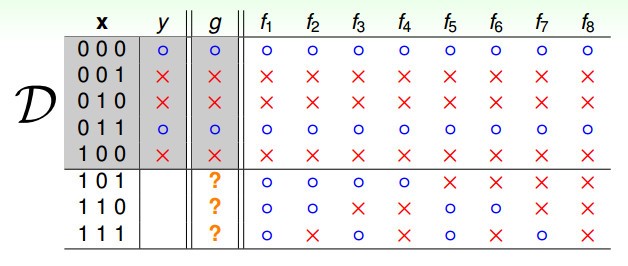
• 如圖所示，輸入為$\mathbf{x}$ 是一個三維向量，且元素之值均為布林值，如果以$D$做為訓練資料(灰色區域)，那麼要預測未知的情況，那請問當$x$為$101$,$110$,$111$的時候，預測輸出$y$是什麼呢？

No free lunch

• 如果我們訓練 $g \in H \ni g(x_n) = y_n$，在不加上任何假設時，無法學習任何東西。

  • 我們看到圖表中，會有$f_1, f_2, \cdots, f_8$ 8種不同的假設（hypothesis）(函數)，所以我們無論預測是哪種輸出，都有可能讓我們的預測是完全錯誤的。這是不是就說明這種條件下，學習器是不可學習的呢？現在我們就從這個角度出發，看看如何訓練我們的學習器，才能讓學習器真正學到有用的知識，進而來產生有效的預測。
  • $g \approx f \text{ inside } D$: sure (樣本內訓練)
  • $g \approx f \text{ outside } D$: No! (樣本外訓練無法保證可逼近真正的函數)

• E.g. 已經序列s前四個值為1,3,5,7，求第5個個值為何?

  • 在不知道真正的generating function時，大多數的人會猜s[5] = 9.
  • 但若真正的generating function為 $\frac{181111}{2}x^4 - 90555 x^3 + \frac{633885}{2} x^2 - 452773 x + 217331$時，s[5]= 217341.

Inference

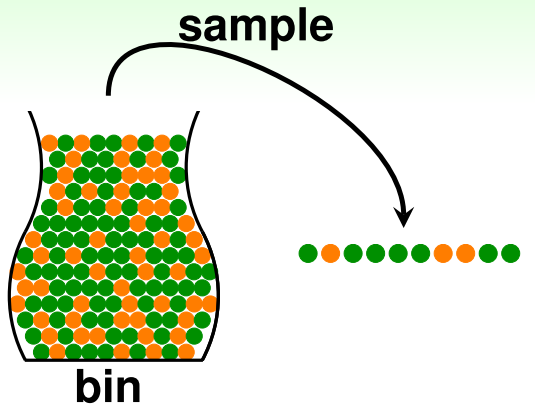
• 我們希望在不知道橘色珠子個數的假設下，估計出橘色珠子的比例為何?
  • 假設罐子中橘色珠子的比例為u, 綠色珠子的比例為1-u，其中u為未知值。
  • 從罐子中抽樣出N個獨立樣本，其中橘色珠子個數的比例為v，綠色珠子的比例為1-v。
  • 則是否可以說樣本中橘色珠子的比例v會接近真實橘色珠子的比例u?
    • No: 可能罐子中綠色珠子佔大多數，但樣本中大多為橘色珠子。
    • Yes：樣本橘色珠子的比例v應該會很接近未知的真實比例u。
    • 為了回答這個問題，必須考慮樣本內與樣本外資料的關係。

Hoeffding's inequality

• 在樣本數 $N$非常大時， 樣本比例 $v$ 在機率上會接近真實的比例 $u$.

  • Hoeffding's inequality: $P[ | v-u| > \epsilon ] \leq 2e^{-2 \epsilon^2 N}$.
  • The statement $v=u$ is probability approiximately correct (PAC).

• Hoeffding's inequality is valid for all $N \in \mathbb{N}, \epsilon \in \mathbb{R}^+$.

  • does not depend on $u$, and no need to know $u$. (此不等式在不須知道真正的機率u即可使用)
  • larger sample size $N$ or looser gap $\epsilon$: higher probabilty for $v=u$.

Error

• 為了描述學習器輸出的假設$h$對真實目標函數$f$的逼近程度，定義兩種錯誤率：

• 真實錯誤(true error)，也稱樣本外錯誤(out-of-sample error)

  • 對於從任意分佈中抽取的所有資料而言。$h$的真實錯誤率是應用$h$到分佈$P$抽取的資料時的期望錯誤率。

• 樣本錯誤 (sample error)，也稱樣本內錯誤(in-sample error)

  • 因為$h$關於$f$的錯誤率不能直接由學習器觀察到($f$未知)。學習器只能觀察到在訓練資料上$h$的性能如何，所以訓練器也只能在此性能基礎上選擇其假設輸出。

  • 使用訓練錯誤率（training error）來指代訓練樣本中被$h$誤分類的資料所占的比例，以區分真實錯誤率。

  • 因此資料集合$D$的樣本錯誤率為資料集合$D$中被$h$誤分類的資料所占的比例。