主成份分析 (Principal component analysis,PCA)
主成分分析可以用來分析調查項目 (或稱為變數,特徵) 間的相關性。 分析後的結果或許可以因為發現某些變數間的相關性, 而縮減調查項目且進一步節省了調查資源
的使用, 或是產生另一組數量較原變數少的新變數, 這個過程即所謂的維度縮減(dimension reduced)。新變數常呈現出新的意義, 是事先分析時不易或無法察覺的, 主成分分析便是從原始變數的資料中, 找到這層關係; 不但保留大部分的 訊息, 也有效的降低變數的數量, 對後續的統計分析, 甚至圖表的表現都很大的助益。
主成分分析經常用於減少資料集合的維數,同時保持資料集合中的對變異數貢獻最大的特徵。這是通過保留訊息量(變異數)較大主成分,忽略訊息量較少的主成分做到的。訊息量大的主成分往往能夠保留住數據的最重要方面。但是,這也不是一定成立,要視具體應用而定。由於主成分分析依賴所給資料,所以資料的準確性對分析結果影響很大。
- 一般會將資料集合表示為矩陣X∈RM×N={x1,x2,⋯,xN},其中row為不同的資料,column為特徵。假設有汽車評分原始資料如下:
| Car |
Design |
Performance |
Space |
| A |
25 |
60 |
58 |
| B |
75 |
35 |
40 |
| C |
50 |
74 |
68 |
| D |
60 |
30 |
40 |
| E |
50 |
80 |
70 |
| F |
80 |
90 |
95 |
| G |
45 |
50 |
50 |
| Avg |
55 |
59.86 |
60.14 |
| Stdev |
18.71 |
22.81 |
19.55 |
- 經過每一個特徵正規化後,即E(xi)=0,Var(xi)=1 ,得下表。
| Car |
Design |
Performance |
Space |
| A |
-1.6 |
0.01 |
-0.11 |
| B |
1.07 |
-1.09 |
-1.03 |
| C |
-0.27 |
0.62 |
0.4 |
| D |
0.27 |
-1.31 |
-1.03 |
| E |
-0.27 |
0.88 |
0.5 |
| F |
1.34 |
1.32 |
1.78 |
| G |
-0.53 |
-0.43 |
-0.52 |
| Avg |
0 |
0 |
0 |
| Stdev |
1 |
1 |
1 |
- 輸入為資料集合X∈RM×N={x1,x2,⋯,xN}。
- 目標是找到縮減維度的資料集合Y∈RM×D={y1,y2,⋯,yD}, D<N。
標準內積與投影
兩個column vectors x, y的內積為:
- ⟨x,y⟩=∥x∥∥y∥cosθ.
- If 0≤θ≤2π,⟨x,y⟩≥0.
- If 2π≤θ≤π,⟨x,y⟩<0.
- 兩向量的標準內積為: ⟨x,y⟩=x⊤y=y⊤x.
-
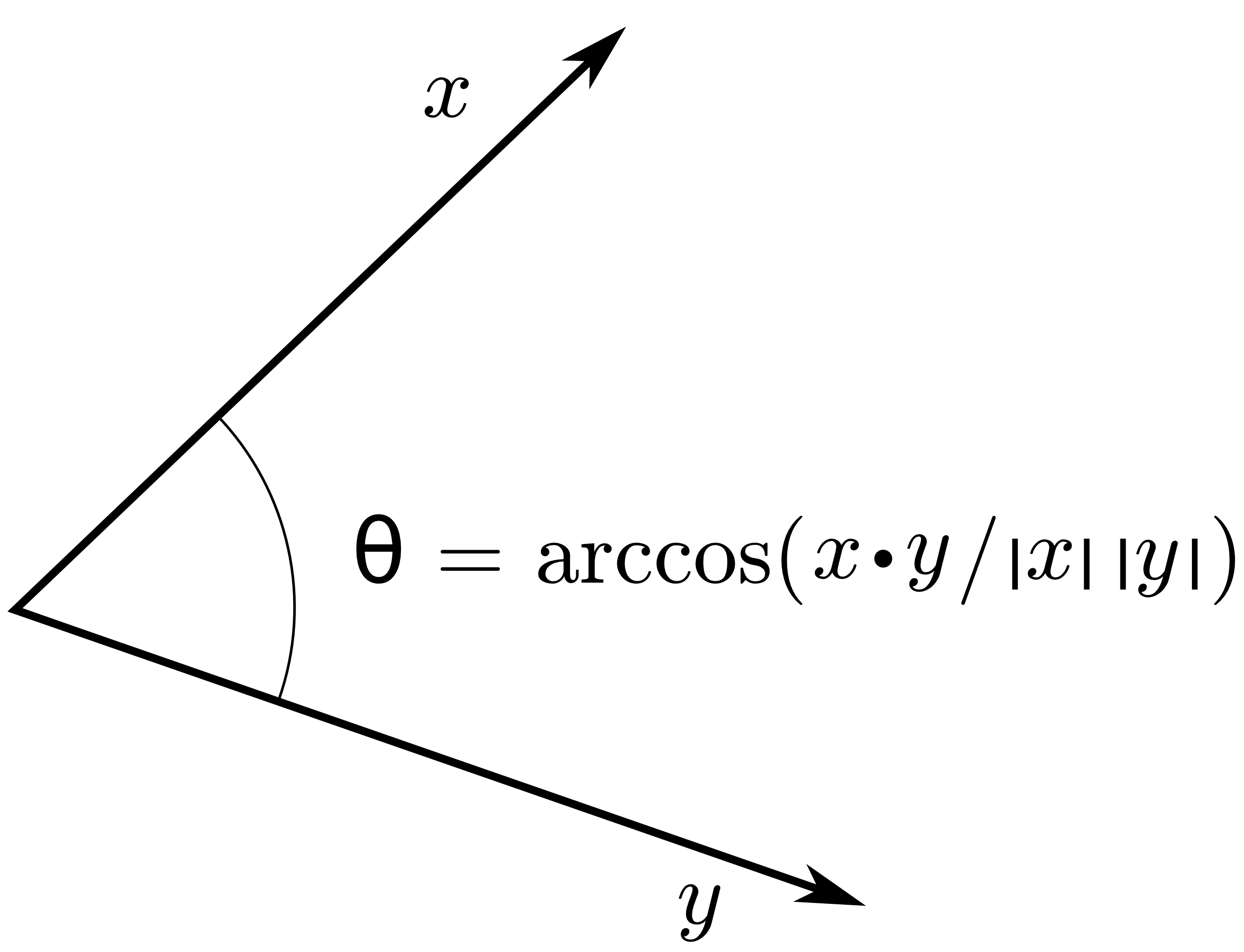 標準內積與投影關係式。
標準內積與投影關係式。
如果將向量x投影至向量y的長度如下:
∥x∥cosθ∥y∥y==[∥x∥∥x∥∥y∥⟨x,y⟩]∥y∥y∥y∥2⟨x,y⟩y.
若y的長度為1時,則x的投影長度為[∥x∥cosθ]∥y∥y=⟨x,y⟩y.
所以向量x投影到單位向量y的座標係數為⟨x,y⟩=x⊤y.
變異數矩陣
- 令X∈RM×N為正規化後的資料矩陣。
- 因此屬性的共變異數矩陣Σ=E[(X⊤−0)(X−0)]=E(X⊤X)∈RN×N.
- 由於PCA考慮的是維度的縮減,而非資料筆數的刪減,因此是使用屬性的共變異數矩陣,而不是資料的共變異數矩陣。
資料旋轉
 資料旋轉。
資料旋轉。
Example
汽車正規化後資料集合可得共變異數矩陣Σ=⎣⎡10.010.20.0110.960.200.961.⎦⎤
對Σ做特徵值分解,得對應的特徵向量與特徵值如下:
| Eigenvalue |
Eigenvector |
| 1.981477 |
(0.15417, 0.69102, 0.70621) |
| 0.995251 |
(0.978264, -0.207074, -0.010942) |
| 0.023272 |
(0.13868, 0.13868, -0.70792) |
- 因此最大變異數投影方向為0.15417 Design +0.69102 Performance +0.70621 Space .
- 因此第二大變異數投影方向為0.978264 Design −0.207074 Performance −0.010942 Space .
- 變異數最小的投影方向為0.13868 Design +0.13868 Performance −0.70792 Space .
- 很明顯可得投影後的變異數大小,與eigenvalue之值大小有關。

