感知機(Perceptron)
- 在1943年,McCulloch和Pitts已提出第一個類神經元的運算模型 。
- 神經心理學家Hebb提出一種理論,他認為學習現象的發生,乃在於神經元間的突觸產生某種變化。
- Rosenblatt將這兩種創新學說結合起來,孕育出所謂的感知機(perceptron)。
- 感知機是由具有可調整的鍵結值 (synaptic weights) 以及閥值 (threshold) 的單一個類神經元 (neuron) 所組成。
- 感知機是各種類神經網路中,最簡單且最早發展出來的類神經網路模型,通常被用來做為分類器(classifier)使用。
感知機基本架構
感知機的基本組成元件為一個具有線性組合功能的累加器,後接一個硬限制器 (hard limiter) 而成.
- 一般說來,若我們設定硬限制器之輸入為正值時,則類神經元的輸出為 +1;反之,若硬限制器之輸入為負值時,則類神經元的輸出為 -1。
分類的判斷規則是:若感知機的輸出為+1,則將其歸類於 C1 群類;若感知機的輸出為 -1,則將其歸類於 C2 群類。
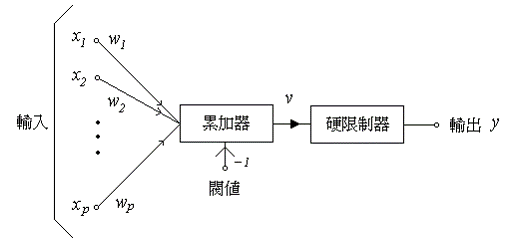
感知機之架構方塊。 判斷規則所劃分的只有兩個判斷區域,我們可以將作為分類依據的超平面定義如下: .
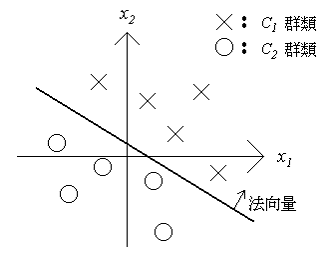
一個具有二維輸入的兩群分類問題。
感知機收斂性
Step 1: 網路初始化
- 以隨機的方式來產生亂數,令為很小的實數,並且將學習循環t定為1。
Step 2: 計算網路輸出值
- 在第t次學習循環時,若輸入向量 x(t),此時類神經元的輸出為: .
Step 3:調整鍵結值向量
Step 4: and goto step 2.
調整後的類神經元,若再用相同的輸入範例來加以測試,則其輸出值會更加地接近期待值.

以幾何觀點來分析感知機之訓練過程;(a)若 d=-1且y=1 ;(b)若 d=1且y=-1 。
*E.g. 資料如下
| 輸入 | 期望輸出 |
|---|---|
| (0,0) | 1 |
| (0,1) | 1 |
| (0,0) | -1 |
| (1,1) | 1 |
- 學習速率 , 連結權重初始值 , activation function為sgn(.), threshold .
- .
- .
- .
- 以此類推。
Widrow-Hoff 法則
- 此種由Widrow和Hoff於1960年提出訓練所謂“適應線性元件” (Adaptive Linear Element 簡稱為 Adaline) 的學習規則,被稱做Widrow-Hoff法則或最小均方誤差法 。
- 基本上 Adaline 和感知機的架構是一樣的,主要的差別在於訓練法則的不同,感知機的訓練目標是減少分類錯誤,而 Adaline 是減少類神經元的真實輸出與期望輸出間的均方誤差。